Math 201 Practice Final
Please work out each of the given problems. Credit will be based on the steps that you show towards the final answer. Show your work.
Problem 1
Match the following hypotheses and estimates with the appropriate test statistic or confidence interval. Explain your reasoning.
i) A confidence interval for a population mean.
ii) A confidence interval for a population proportion.
iii) A confidence interval for the difference between two independent population means
iv) A confidence interval for the difference between two population proportions.
v) A confidence interval for paired differences (dependent samples).
vi) A confidence interval for the value of y given a value of x using a regression line.
vii) A hypothesis test for a population mean.
viii) A hypothesis test for a population proportion.
ix) A hypothesis test for the difference between two independent population means
x) A hypothesis test for the difference between two population proportions.
xi) A hypothesis test for paired differences (dependent samples).
xii) Chi squared test for independence.
xiii) Chi squared test for goodness of fit.
A. Are automobile prices higher in South Lake Tahoe then in Sacramento. Fifty Subaru Legacy's from the South Tahoe dealership and fifty from the Sacramento dealership were sold last month and recorded.
ix. There are two samples, each with continuous data and cannot be paired.
B. Does the color of the paper used for a final exam influence performance? 200 students were randomly given the same test on blue, red, and white paper. The number of A's, B's, C's, D's and F's for each color were tabulated.
xii. There are multiple types and the counts are taken of each.
C. Is honey a better medicine for small wounds than conventional salves? Currently 9% of the wounds that are treated with conventional salves end up infected. 150 wounds in a study group were treated with honey.
viii. There is only one sample and the data is Boolean.
D. How much of food that you buy ends up being thrown out? A refrigerator was monitored that had 45 perishable items.
ii. The data is Boolean (either spoils or does not spoil) and there is only one sample taken.
E. How long can you expect to live if your cholesterol level is 230? Data has been taken from 45,000 people with varying levels of cholesterol.
vi. We are given a value for x (230) and are interested in y.
F. How much better has the NASDAQ done than the Dow Jones Industrial Average this year? The daily point gains and losses have been charted since January 2.
v. We have two sets of data that can be paired by date.
G. What are the low and high estimates for the number of Kokanee salmon that will run in Trout Creek this fall? Data has been collected over the last forty years.
i. There is one sample of a continuous random variable.
Problem 2 Your business is being investigated about unfair promotion practices with regard to race. Your policy is to promote 20% of your employees. Your current staff consists of 200 Caucasians, 50 Hispanics, 30 African Americans, and 20 classified as other. Below is a table that shows the number of employees that were promoted last year.
| Caucasian | Hispanic | African American | Other |
| 50 | 6 | 3 | 1 |
what can be concluded at the 5% level?
We perform a Chi square goodness of fit test. Our hypotheses are
H0: The population fits the given distribution
H1: The population has a different distribution
We create the table
| Item | O | E | (O - E)2 | (O - E)2/E |
| Caucasian | 50 | 40 | 100 | 2.5 |
| Hispanic | 6 | 10 | 16 | 1.6 |
| African American | 3 | 6 | 9 | 1.5 |
| Other | 1 | 4 | 9 | 2.25 |
| 60 | 60 | 7.85 |
There are 4 - 1 = 3 degrees of freedom. We go to the table and find that the Chi square critical value is 7.81. Since
7.85 > 7.81
we reject the null hypothesis and conclude that there is sufficient evidence to conclude that true hiring practices differ from what is claimed.
Problem 3 A certain model of car comes in a two-door version, a four door version, and a hatchback version. Each version can be equipped with either an automatic transmission or a manual transmission. The accompanying table gives the relevant proportions.
| TD | FD | HB | |
| A | 0.32 | 0.27 | 0.18 |
| M | 0.08 | 0.04 | 0.11 |
A customer who has purchased one of these cars is randomly selected.
A. What is the probability that the customer purchased a car with an automatic transmission? A four-door car?
P(A) = 0.32 + 0.27 + 0.18 = 0.77
P(FD) = 0.27 + 0.04 = 0.31
There is a 77% chance that the customer purchased a car with automatic transmission and a 31% chance that the customer purchased a car with four doors.
B. Given that the customer purchased a four door car, what is the probability that is has an automatic transmission?
We compute
P(A and
FD)
0.27
P(A|FD) =
=
= 0.87
P(FD)
0.31
If we know that the customer purchased a four door car, then there is an 87% chance that this car had automatic transmission.
C. Giver that the customer did not purchase a hatchback, what is the probability that the car has a manual transmission?
We compute
P(M and not HB)
0.08 + 0.04
P(M|not HB) =
=
= 0.17
P(not HB)
0.08 + 0.04 + 0.32 + 0.27
If we know that the customer did not purchase a hatchback, then there is an 17% chance that this car had manual transmission.
D. If 8 cars were sold, where is the probability that exactly 6 of them were two doors with automatic transmission?
We solve this using the binomial distribution formula. We get
C8,6(0.32)6(0.68)2 = 0.0139
There is a 1.4% chance that exactly six of the cars had automatic transmission.
Problem 4 You want to construct a confidence interval for the
percent of registered voters who are planning on voting for George Bush for
president for his second term. You want to have a margin of error of
![]() 0.03.
0.03.
A. How many registered voters should you survey (use a = 0.05)?
Since we do not have a preliminary estimate we use the formula
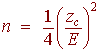
We get
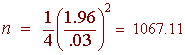
We should survey 1068 registered voters
B. Suppose that you conducted this survey (as in part A) and found that 52% of the respondents intended to vote for George Bush. Construct the appropriate 90% confidence interval. Interpret this interval. How would the Bush campaign react to this confidence interval?
We have
zc = 1.645 n = 1,068 p = .52 q = .48
The 90% confidence interval is
![]()
We can conclude that there is a 90% confidence that between 49% and 55% of the voters intend to vote for Bush for a second term. Since this interval contains numbers less than 50%, he should attempt to woo more voters.
Problem 5 For the following please answer true or false. If true explain why. If false explain why or provide a counter example.
A. To provide a confidence interval for a population proportion, if the sample size is 18, it is appropriate to use a t-statistic since the z-statistic is used only for large samples.
False, the t-statistic can not be used for Boolean data.
B. For a large sample, of the mean, the median, and the standard deviation, only two of these will be highly affected by an addition of an extreme outlier.
True, the median is not highly affected by extreme outliers.
C. No matter how the population data is distributed, the distribution of all possible samples of size 500 will be approximately normal with approximately the same mean and standard deviation as the population mean and standard deviation.
False, the standard deviation of the sampling distribution is equal to the standard deviation of the original distribution divided by the square root of 500.
Problem 6 Data was collected to study the effect of alcohol on reaction time. Forty participants were given various amounts of alcohol and then took a test to see how many milliseconds it took to press a button upon seeing headlights. The scatter diagram is shown below.
A. Given an approximate equation of the regression line. Interpret the slope and the y-intercept.
First we eyeball the line. Then find two points on the line.
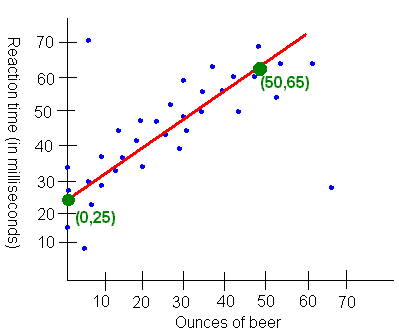
The y-intercept is about 25 and the slope is about
65 - 25
m =
= .8
50 - 0
The equation is
y = 25 + .8 x
The y-intercept tells us that without drinking any alcohol, the reaction time is about 25 milliseconds. The slope tells us that for every ounce of alcohol a person drinks, reaction time goes up by about 0.8 milliseconds.
B. Give an approximation of the correlation coefficient. Explain using a complete sentence why you chose this number.
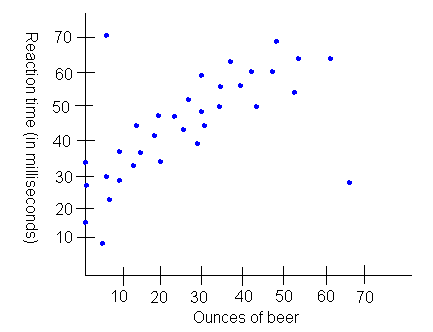
The correlation is probably around 0.8 since the data generally follows a linear model, but not perfectly. Since the slope is positive, so is the correlation coefficient.
Problem 7
Twenty-five students took the first midterm exam. The number of minutes that they each took are shown below.
35, 45, 48, 50, 50, 52, 60, 61, 64, 70, 72, 75, 78, 78, 81, 83, 84, 87, 88, 88, 89, 90, 90, 90, 90
A. Construct a stem and leaf diagram for this data
We make a stem and leaf diagram with the stems representing the tens digit and the leaves representing the ones.
3
|| 5
4 || 5 8
5 || 0 0 2
6 || 0 1 4
7 || 0 2 5 8 8
8 || 1 3 4 7 8 8 9
9 || 0 0 0 0
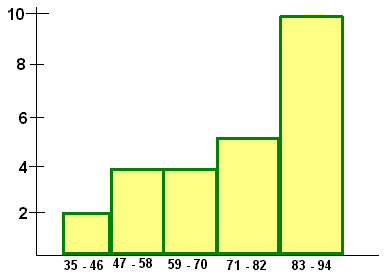
B. Construct a histogram for this data using 5 classes.
We find the class width by taking the range, dividing by 5 and increase the result to the nearest whole number.
90 - 35
+ 1 = 12
5
Next make a frequency distribution table
| Class Interval | Frequency |
| 35 - 46 | 2 |
| 47 - 58 | 4 |
| 59 - 70 | 4 |
| 71 - 82 | 5 |
| 82 - 93 | 10 |
The histogram is shown below
C. You took one hour to complete the exam. What is your percentile?
We are looking at the percentile that corresponds with 60 minutes. There are 6 times below 60. We calculate
6/25 x 100% = 24%
You are in the 24th percentile.
D. What is the mode?
Solution The mode is the value that occurs the most, namely 90.
E. If the student who took 35 minutes for the exam is disregarded, would the standard deviation decrease, increase, or stay the same. Explain.
Solution The standard deviation would decrease, since more of the data would fall closer to the mean.
Problem 8
A study was done to see the relationship between the type of town and the quality of service. An index was used with 100 meaning average service and larger numbers above average. The table below displays the results of the survey.
| Police | Fire Department | Libraries | Schools | |
| Urban | 110 | 115 | 140 | 82 |
| Rural | 132 | 128 | 130 | 84 |
| Suburban | 95 | 102 | 118 | 92 |
- List the factors and the number of levels of each factor.
Solution
There are 2 factors: Type of town with three levels and type of public service with four levels.
- Assume that there is no interaction between the factors.
Determine if there is a difference in population mean index based on town
type. Use a level of significance of 0.05.
Make sure you state the null and alternative hypothesis and state your
conclusions using a complete sentence in the context of the question.
Solution
H0: There is no difference in mean public service based on town type.
H1: At least two town types have different mean public service ratings.
Since the P-Value is 0.18, we do not have sufficient evidence to make a conclusion about town type being a factor in determining that there is a difference in the levels of each public service. That is it is plausible that all town types have the same public service ratings.
- Determine if there is a difference in population mean
index bases on public service. Use a level of significance of
0.05.Make sure you state the null and alternative
hypothesis and state your conclusions using a complete sentence in the context
of the question.
Solution
H0: There is no difference in mean rating based on the type of public service.
H1: At least two public services have different mean ratings.
Since the P-Value is 0.02, we do have sufficient evidence to show that at least two public services give a different mean rating.