Hypothesis Testing For a Population Mean

 

The Idea of Hypothesis Testing 

Suppose we want to show that only children have an average higher cholesterol level than the national average.  It is known that the mean cholesterol level for all Americans is 190.  Construct the relevant hypothesis test:

        H0: m = 190 


        H1: m > 190 

 

We test 100 only children and find that

        x = 198 

and suppose we know the population standard deviation

        s = 15.

Do we have evidence to suggest that only children have an average higher cholesterol level than the national average?  We have

       

z is called the test statistic.

Since z is so high, the probability that Ho is true is so small that we decide to reject H0 and accept H1.  Therefore, we can conclude that only children have a higher average cholesterol level than the national average.

 

 

Rejection Regions

Suppose that a = .05.  We can draw the appropriate picture and find the z score for -.025 and .025.  We call the outside regions the rejection regions.  

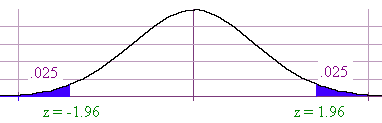
We call the blue areas the rejection region since if the value of z falls in these regions, we can say that the null hypothesis is very unlikely so we can reject the null hypothesis

 

Example

50 smokers were questioned about the number of hours they sleep each day.  We want to test the hypothesis that the smokers need less sleep than the general public which needs an average of 7.7 hours of sleep.  We follow the steps below.

 

  1. Compute a rejection region for a significance level of .05.  

  2. If the sample mean is 7.5 and the population standard deviation is 0.5, what can you conclude?

 

Solution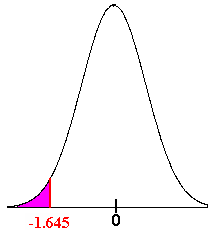

First, we write write down the null and alternative hypotheses

H0:  m  =  7.7            H1:  m  < 7.7

This is a left tailed test.  The z-score that corresponds to .05 is -1.645.  The critical region is the area that lies to the left of -1.645.  If the z-value is less than -1.645 there we will reject the null hypothesis and accept the alternative hypothesis.  If it is greater than -1.645, we will fail to reject the null hypothesis and say that the test was not statistically significant.

We have

       

Since -2.83 is to the left of -1.645, it is in the critical region.  Hence we reject the null hypothesis and accept the alternative hypothesis.  We can conclude that smokers need less sleep.

 

p-values

There is another way to interpret the test statistic.  In hypothesis testing, we make a yes or no decision without discussing borderline cases.  For example with a = .06, a two tailed test will indicate rejection of H0 for a test statistic of z = 2 or for z = 6, but z = 6 is much stronger evidence than z = 2.  To show this difference we write the p-value which is the lowest significance level such that we will still reject Ho.  For a two tailed test, we use twice the table value to find p, and for a one tailed test, we use the table value.  

 

Example:

Suppose that we want to test the hypothesis with a significance level of .05 that the climate has changed since industrializatoin.  Suppose that the mean temperature throughout history is 50 degrees.  During the last 40 years, the mean temperature has been 51 degrees and suppose the population standard deviation is 2 degrees.  What can we conclude?  

We have

        H0:  m = 50

        H1:  m 50

We compute the z score:

       

The table gives us .9992

so that 

        p = (1 - .9992)(2) = .002

since 

        .002 < .05 

we can conclude that there has been a change in temperature. 

Note that small p-values will result in a rejection of H0 and large p-values will result in failing to reject H0. 

Back to the Hypothesis Testing Home Page

Back to the Elementary Statistics (Math 201) Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions