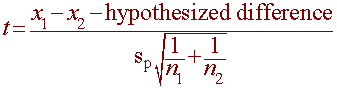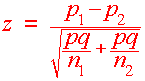Difference Between Means

Difference Between Means

Hypothesis Testing of the Difference Between Two Means

Do employees perform better at work with music playing. The music was turned on during the working hours of a business with 45 employees. There productivity level averaged 5.2 with a standard deviation of 2.4. On a different day the music was turned off and there were 40 workers. The workers' productivity level averaged 4.8 with a standard deviation of 1.2. What can we conclude at the .05 level?

Solution

We first develop the hypotheses

H₀: m₁ - m₂ = 0

H₁: m₁ - m₂ > 0

Next we need to find the standard deviation. Recall from before, we had that the mean of the difference is

m_x = m₁ - m₂

and the standard deviation is

s_x =

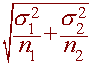
We can substitute the sample means and sample standard deviations for a point estimate of the population means and standard deviations. We have

and

Now we can calculate the t-score. We have

                    0.4
        t =                       = 0.988
                   0.405

To calculate the degrees of freedom, we can take the smaller of the two numbers n₁ - 1 and n₂ - 1. So in this example we use 39 degrees of freedom. The t-table gives a value of 1.690 for the t_.95 value. Notice that 0.988 is still smaller than 1.690 and the result is the same. Since the t-score is smaller than 1.690, we fail to reject the null hypothesis and state that there is insufficient evidence to make a conclusion about employees performing better at work with music playing.

Hypothesis Testing For a Difference Between Means for Small Samples Using Pooled Standard Deviations (Optional)

Recall that for small samples we need to make the following assumptions:

Random unbiased sample.
Both population distributions are normal.
The two standard deviations are equal.

If we know s, then the sampling standard deviation is:

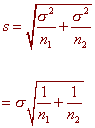
If we do not know s then we use the pooled standard deviation.

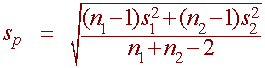
Putting this together with hypothesis testing we can find the t-statistic.

and use n₁ + n₂ - 2 degrees of freedom.

Example

Nine dogs and ten cats were tested to determine if there is a difference in the average number of days that the animal can survive without food. The dogs averaged 11 days with a standard deviation of 2 days while the cats averaged 12 days with a standard deviation of 3 days. What can be concluded? (Use a = .05)

Solution

We write:

H₀: m_dog - m_cat = 0

H₁: m_dog - m_cat 0

We have:

n₁ = 9, n₂ = 10

x₁ = 11, x₂ = 12

s₁ = 2, s₂ = 3

so that

and

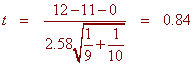
The t-critical value corresponding to a = .05 with 10 + 9 - 2 = 17 degrees of freedom is 2.11 which is greater than .84. Hence we fail to reject the null hypothesis and conclude that there is not sufficient evidence to suggest that there is a difference between the mean starvation time for cats and dogs.

Hypothesis Testing for a Difference Between Proportions

Inferences on the Difference Between Population Proportions

If two samples are counted independently of each other we use the test statistic:

where
                    r₁ + r₂
          p =
                    n₁ + n₂
and
          q = 1 - p

Example

Is the severity of the drug problem in high school the same for boys and girls? 85 boys and 70 girls were questioned and 34 of the boys and 14 of the girls admitted to having tried some sort of drug. What can be concluded at the .05 level?

Solution

The hypotheses are

H₀: p₁ - p₂ = 0

H₁: p₁ - p₂ 0

We have

p₁ = 34/85 = 0.4 p₂ = 14/70 = 0.2

p = 48/155 = 0.31 q = 0.69

Now compute the z-score

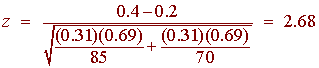
Since we are using a significance level of .05 and it is a two tailed test, the critical value is 1.96. Clearly 2.68 is in the critical region, hence we can reject the null hypothesis and accept the alternative hypothesis and conclude that gender does make a difference for drug use. Notice that the P-Value is

P = 2(1 - .9963) = 0.0074

is less than .05. Yet another way to see that we reject the null hypothesis.

Back to the Hypothesis Testing Home Page

Back to the Elementary Statistics (Math 201) Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions