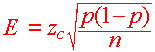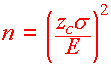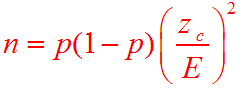Confidence Intervals For Proportions and 

Choosing the Sample Size

A Large Sample Confidence Interval for a Population Proportion

Recall that a confidence interval for a population mean is given by

Confidence Interval for a Population Mean                                          zc s                           x

We can make a similar construction for a confidence interval for a population proportion.  Instead of x, we can use p and instead of s, we use , hence, we can write the confidence interval for a large sample proportion as

Confidence Interval Margin of Error for a Population Proportion

Example

1000 randomly selected Americans were asked if they believed the minimum wage should be raised.  600 said yes.  Construct a 95% confidence interval for the proportion of Americans who believe that the minimum wage should be raised.

Solution:  

We have 

        p = 600/1000 = .6         z_c = 1.96         and     n = 1000  

We calculate:

Hence we can conclude that between 57 and 63 percent of all Americans agree with the proposal. In other words, with a margin of error of .03 , 60% agree.

Calculating n for Estimating a Mean

Example

Suppose that you were interested in the average number of units that students take at a two year college to get an AA degree.  Suppose you wanted to find a 95% confidence interval with a margin of error of  .5 for m knowing s = 10.  How many people should we ask?

Solution

Solving for n in

        Margin of Error  =  E  = z_c s/

we have

        E =  z_cs

                          z_c s  
          =                     
                            E

Squaring both sides, we get

We use the formula:  

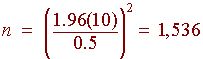
Example

A Subaru dealer wants to find out the age of their customers  (for advertising purposes).  They want the margin of error to be 3 years old.  If they want a 90% confidence interval, how many people do they need to know about?

Solution: 

We have 

        E = 3,       z_c = 1.65

but there is no way of finding sigma exactly.  They use the following reasoning: most car customers are between 16 and 68 years old hence the range is 

        Range  =  68 - 16  =  52

The range covers about four standard deviations hence one standard deviation is about

        s  @  52/4  =  13

We can now calculate n:

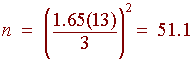
Hence the dealer should survey at least 52 people.

Finding n to Estimate a Proportion

Example 

Suppose that you are in charge to see if dropping a computer will damage it.  You want to find the proportion of computers that break.  If you want a 90% confidence interval for this proportion, with a margin of error of   4%, How many computers should you drop?

Solution

The formula states that

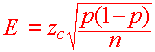
Squaring both sides, we get that

                      z_c² p(1 - p)
          E²  =                              
                             n

Multiplying by n, we get

        nE²  =  z_c²[p(1 - p)]

This is the formula for finding n.

Since we do not know p, we use .5  ( A conservative estimate)

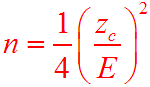
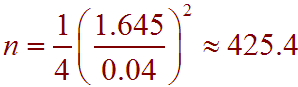          We round 425.4 up for greater accuracy

We will need to drop at least 426 computers.  This could get expensive.

Handout of more examples and exercises on finding the sample size

Back to the Estimation Home Page

Back to the Elementary Statistics (Math 201) Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions