Mean and Standard Deviation for Grouped Data

m and s for Grouped Data

Calculating the Mean from a Frequency Distribution

Since calculating the mean and standard deviation is tedious, we can save some of this work when we have a frequency distribution. Suppose we were interested in how many siblings are in statistics students' families. We come up with a frequency distribution table below.

Number of Children	1	2	3	4	5	6	7
Frequency	5	12	8	3	0	0	1

Notice that since there are 29 respondents, calculating the mean would be very tedious. Instead, we see that there are five ones, 12 twos, 8 threes, 3 fours, and 1 seven. Hence the total count of siblings is

1(5) + 2(12) + 3(8) + 4(3) + 7(1) = 72

Now divide by the number of respondents to get the mean.

                   72
        m =            = 2.5
                  29

Extending the Frequency Distribution Table

Just as with the mean formula, there is an easier way to compute the standard deviation given a frequency distribution table. We extend the table as follows:

Number of Children (x)	Frequency (f)	xf	x²f
1	5	5	5
2	12	24	48
3	8	24	72
4	3	12	48
5	0	0	0
6	0	0	0
7	1	7	49
Totals	Sf = 29	Sxf = 72	Sx²f = 222

Next we calculate

                                   (Sxf)²                  (72)²
        SS_x = Sx²f -                 = 222 -
                                      n                        29

= 43.24

Now finally apply the formula

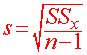
to get

Click here for an applet that finds statistics from grouped data.

Weighted Averages

Sometimes instead of the simple mean, we want to weight certain outcomes higher then others. For example, for your statistics class, the following percentages are given

Homework = 150

Midterm = 450

Project = 100

Final = 300

Suppose that you received an 88% on your homework, a 97% on your midterms, a 98% on your project and an 78% on your final. What is your average for you class?

To compute the weighted average, we use the formula

                                                Sxw
        Weighted Average =
                                                Sw

We have

Sxw = .88(150) + .97(450) + .98(100) + .78(300) = 900.5

and

Sw = 150 + 450 + 100 + 300 = 1000

Now divide to get your weighted average

            900.5
                        = .9005
            1000

You squeaked by with an "A".

Back to the Descriptive Statistics Home Page

Back to the Elementary Statistics (Math 201) Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions