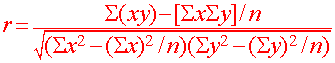Correlation

Residuals

Suppose that the average lifespan for people who smoke is:


Packs Per Week Life Span
1 72
2 70
3 69
5 68

 

We can calculate the least squares regression line:

        y = 73 - 1.3x

We define the first residual to be the difference between the first lifespan and the first estimated lifespan:

        72 - (73 - 1.3(1)) = 0.3

the second residual as:

        70 - (73 - 1.3(2)) = -0.4

the third as:

        69 - (73 - 1.3(3)) = -0.1

and the fourth as

        68 - (73 - 1.3(5)) = 1.5

in general we have the residual is


yi  - y   =   yi  - (a + bxi)


Coefficient of determination: r2

 We define the coefficient of determination as an indication of how linear the data is.  r2 has the following properties:

 

Properties of the Coefficient of Determination

 

  1. r2 is between 0 and 1.

  2. If  r2  =  1 then all points lie on a line.  (perfectly linear)

  3. If r2  =  0 then the regression line is a useless indicator for predicting y values.

Construction

To compute r2, do the following:

 

  1. Compute the sum of the squares of the residuals:  SSResid

  2. Compute Sy2 and (Sy)2.  We say that 

            SSTo = Sy2 - (S y)2/n

  3. Compute 

            1 - SSResid/SSto

    This is r2 .

 

If we multiply r2 by 100%, we arrive at the percent of the observed variation attributable to the linear relationship.  

 

 

Correlation:   r

If we want to determine not just if they are linearly related, but also want to know whether there is a positive relationship or a negative relationship (b> 0 or b<0) and want the calculation unitless, we compute Pearson's correlation coefficient r


 

We have 

        r2  =  r2  

that is the square of the correlation coefficient is equal to the coefficient of determination.  

  • If r  <  0 then they are negatively correlated.

  • If r > 0 then they are positively correlated.

 

We say that the correlation is

 

  1.   strong if |r| >.8

  2. middle if .5 < |r| < .8 and 

  3. weak otherwise.  

 

 

Correlation does not imply causation.  For example there may be a strong correlation between grayness in hair and wrinkles, but having gray hair does not cause one to have wrinkles.

 

Back to the Regression and Nonparametric Home Page

Back to the Elementary Statistics (Math 201) Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions