Test for Homogeneity

Summary:  This module describes how the chi-square distribution can be used to test for homogeneity.

The Goodness of Fit test can be used to decide whether a population fits a given distribution, but the Goodness of Fit test will not suffice to compare whether two populations follow the same unknown distribution.  A different test, called the Test for Homogeneity, can be used to make a conclusion about whether two populations have the same distribution.  To calculate the test statistic for a test for homogeneity, follow the same procedure as with the c2 test for independence.

Here is a summary of the Test for Homogeneity:

Hypotheses

H0:  The distributions of the two populations are the same.
Ha:  The distributions of the two populations are not the same.

Test Statistic

Uses a c2 statistic.  It is computed in the same way as the test for independence. 

Requirements

All values in the table must be greater than or equal to 5.

Common Uses

Comparing two populations.  For example:  men vs women, before vs. after, east vs. west.

  The variable is categorical with more than two possible response values.

 

EXAMPLE 1

Do male and female college students have the same distribution of living conditions?  Use a level of significance of 0.05.  Suppose that 250 randomly selected male college students and 300 randomly selected female college students were asked about their living conditions:  Dorm, Apartment, With Parents, Other.  The results are shown in the table below:

  Dorm Apartment With Parents Other
Male 72 84 49 45
Female 91 86 88 35

Solution

The null and alternative hypotheses are:

H0: The distribution of living conditions for male college students is the same as the distribution of living conditions for female college students.
Ha: The distribution of living conditions for male college students is the not the same as the distribution of living conditions for female college students.

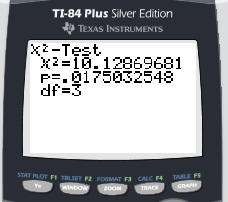
To compute the test statistic, follow the same process as with the test for independence.  Here there are 2 rows and 4 columns.  Note that the degrees of freedom for this test is

          df  =  the number of columns - 1  =  3

To the right is the readout from a TI 84+.TI84: Chi-Square 10.13, p = 0.0175, df = 3  The c2 test statistic is about 10.13 and the p-value is 0.0175.  As with all hypothesis tests, reject the null hypothesis if the p-value is less than the level of significance and fail to reject the null hypothesis if the p-value is greater than the level of significance.  In this case,

          p-value = 0.0175 < 0.05 = Level of Significance

Therefore, reject the null hypothesis and accept the alternative hypothesis.  You can conclude that the distributions of living conditions for male and female college students are not the same. 

Notice that the conclusion is only that the distributions are not the same.  One cannot use the test for homogeneity to make any conclusions about how they differ.

EXAMPLE 2

Both before and after a recent earthquake surveys were conducted asking voters which of the three candidates they planned on voting for in the upcoming city council election.  Has there been a change since the earthquake?  Use a level of significance of 0.05.  The table below shows the results of the survey.

  Perez Chung Stevens
Before 167 128 135
After 214 197 225

Solution

The null and alternative hypotheses are:

H0: The distribution of voter preferences was the same before and after the earthquake.
Ha: The distribution of voter preferences was not the same before and after the earthquake.

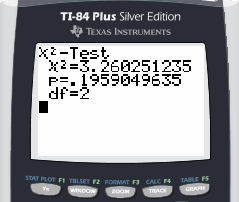
This table has 2 rows and 3 columns.  The degrees of freedom for this test isTI 84 Chi-Square = 3.26, p-value = 0.196, df = 2

          df  =  the number of columns - 1  =  2

To the right is the readout from a TI 84+.  The c2 test statistic is about 3.26 and the p-value is 0.196.  The inequality is

          p-value = 0.196 > 0.05 = Level of Significance

Therefore, fail to reject the null hypothesis.  There is insufficient evidence to make a conclusion about whether the distribution of voter preferences differs before and after the earthquake.
 

Video on Test for Homogeneity

Summary of a c2-Tests

You have seen the a c2 test statistic used in three different circumstances. Below is a summary that will help you decide which c2 test is the appropriate one to use.

  • Goodness of Fit:  Use the Goodness of Fit Test when you want to decide whether a population with unknown distribution "fits" a known distribution.  In this case there will be a single qualitative survey question or a single outcome of an experiment from a single population.  Goodness of fit is typically used to see if the population is uniform (all outcomes occur with equal frequency), the population is normal, or the population is the same as another population with known distribution.  The null and alternative hypotheses are:
    • H0:  The population fits the given distribution.
    • Ha:  The population does not fit the given distribution.
  • Independence:  Use the Test for Independence when you want to decide whether two variables are independent or dependent.  In this case there will be two qualitative survey questions or experiments and a contingency table will be constructed.  The goal is to see if the two variables are unrelated (independent) or related (dependent).  The null and alternative hypotheses are:
    • H0:  The two variables are independent.
    • Ha:  The two variables are dependent.
  • Homogeneity:  Use the Test for Homogeneity when you want to decide if two populations with unknown distribution have the same distribution as each other.  In this case there will be a single qualitative survey question or experiment given to two different populations.  The null and alternative hypotheses are:
    • H0:  The two populations follow the same distribution.
    • Ha:  The two populations have different distributions.