Confidence Intervals for a Mean
Point Estimations
Usually, we do not know the population mean and standard deviation. Our goal is to estimate these numbers. The standard way to accomplish this is to use the sample mean and standard deviation as a best guess for the true population mean and standard deviation. We call this "best guess" a point estimate.
A Point Estimate is a statistic that gives a plausible estimate for the value in question.
Example:
x is a point estimate for m
s is a point estimate for s
A point estimate is unbiased if its mean represents the value that it is estimating.
Confidence Intervals
We are not only interested in finding the point estimate for the mean, but also determining how accurate the point estimate is. The Central Limit Theorem plays a key role here. We assume that the sample standard deviation is close to the population standard deviation (which will almost always be true for large samples). Then the Central Limit Theorem tells us that the standard deviation of the sampling distribution is
![]()
We will be interested in finding an interval around x such that there is a large probability that the actual mean falls inside of this interval. This interval is called a confidence interval and the large probability is called the confidence level.
Example
Suppose that we check for clarity in 50 locations in Lake Tahoe and discover that the average depth of clarity of the lake is 14 feet. Suppose that we know that the standard deviation for the entire lake's depth is 2 feet. What can we conclude about the average clarity of the lake with a 95% confidence level?
Solution
We can use x to provide a point estimate for m. How accurate is x as a point estimate? We construct a 95% confidence interval for m as follows. We draw the picture and realize that we need to use the table to find the z-score associated to the probability of .025 (there is .025 to the left and .025 to the right).
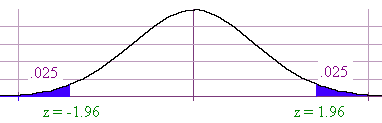
We arrive at z = -1.96. Now we solve for x:
x - 14 x -
14
-1.96 =
=
2/
![]() 0.28
0.28
x - 14 = -0.55
We say that ![]() 0.55 is the margin of error.
0.55 is the margin of error.
We have that a 95% confidence interval for the mean clarity is
(13.45,14.55)
In other words there is a 95% chance that the mean clarity is between 13.45 and 14.55.
In general if zc is the z value associated with c% then a c% confidence interval for the mean is
![]()
Confidence Interval for a Mean When the Population Standard Deviation is Unknown
When the population is normal or if the sample size is large, then the sampling distribution will also be normal, but the use of s to replace s is not that accurate. The smaller the sample size the worse the approximation will be. Hence we can expect that some adjustment will be made based on the sample size. The adjustment we make is that we do not use the normal curve for this approximation. Instead, we use the Student t distribution that is based on the sample size. We proceed as before, but we change the table that we use. This distribution looks like the normal distribution, but as the sample size decreases it spreads out. For large n it nearly matches the normal curve. We say that the distribution has n - 1 degrees of freedom.
Example
Suppose that we conduct a survey of 19 millionaires to find out what percent of their income the average millionaire donates to charity. We discover that the mean percent is 15 with a standard deviation of 5 percent. Find a 95% confidence interval for the mean percent. Assume that the distribution of all charity percents is approximately normal.
Solution
We use the formula:
![]() (Notice the t instead of the z and s instead of
s)
(Notice the t instead of the z and s instead of
s)
We get
15 ![]() tc 5 /
tc 5 /
![]()
Since n = 19, there are 18 degrees of freedom. Using the table in the back of the book, we have that
tc = 2.10
Hence the margin of error is
![]() 2.10
(5) /
2.10
(5) / ![]() =
= ![]() 2.4
2.4
We can conclude with 95% confidence that the millionaires donate between
12.6% and 17.4% of their income to charity.
Handout on finding the sample size needed for a confidence interval for a mean
Back to the Estimation Home Page
Back to the Elementary Statistics (Math 201) Home Page