Rounding and Estimation

 

  1. The Number Line

    On of the most useful ways of displaying numbers is the number line which is defined as follows.  First draw a line.  then label a number on the line (usually 0).  To the left of that number represents values below and to the right of that number represents values above that number.  We usually make sure that the line has uniform scale.  For example if 0 is the central point, and 1 is two cm from 0, than 2 should be 4 cm from zero.  

    Example

           

  2. Rounding Whole Numbers

    According to the census bureau, the population of the United States is 285,868,158.  Although this number is precise, it is cumbersome and difficult to remember.  Instead of using this number, we would like to be able to write an estimate that contains only the leftmost digit.  We could use 200,000,000, but there is a better estimate.  If we place this number on the number line, we see that 285,868,158 is between 200,000,000 and 300,000,000.  However the population is closer to 300,000,000.



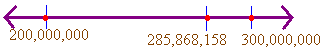
    We say that to the nearest hundred thousand, the population of the US is 300,000,000.

    Without graphing how can we determine how to round?  If the number is halfway between or greater, we round up to the larger number.  Otherwise we round down to the smaller number. We can look to the second digit to the left as the determining factor.  Since 5 is the half way point from 1 to 10, we follow the rules below:

    Rounding a Whole Number

    1. If the second digit to the left is less than 5 we make not change to the round off digit.
    2. If the second digit to the left is 5 or more we add one to the round off digit.

    Then change all the digits except the round off digit to zeros.

 

Examples

  1. Round 246 to the nearest hundred.

    Solution

    The hundreds digit is the 2, the next digit is 4 which is less than 5.  By rule 1. we do not change the 2 and we replace the 4 and 6 with zeros.

            200

  2. Round 76,779 to the nearest ten thousand.

    Solution

    The ten thousands digit is 7 and the next digit is 6 which is greater than 5.  By rule 2. we change the 7 to an 8 and the rest of the numbers become zeros.

            80,000
  3. Round 43,981 to the nearest thousand.

    Solution

    The thousands digit is 3, and the number to its right is 9 which is greater than 5.  We change the 3 to a 4 and everything to its right to a zero

            44,000

Exercises

  1. Round 5,342,167 to the nearest million        5,000,000

  2. Round 28,194 to the nearest hundred    28,200

 

  1. Rounding and Arithmetic

    Example

    Suppose you are planning to have a party for 293 guests at a reception hall that charges $42 per person.  If you want to figure the total bill, you could multiply the two numbers.  However, if you just want a ball park figure, there is an easy way to quickly find the solution.  We round each number so that only the left digit is nonzero.  We can say that there are about 300 guests at $40 per person.  Now the multiplication becomes easy

            300
           x 40
          12,000

    We can conclude that the total cost will be about $12,000.

    The actual amount is $12,306 which is pretty close to the estimate.


    We can use the same method to approximate any calculation.

    Example

    Use Rounding to estimate

            592 + 421 + 389 + 830

    Solution

    We round each of the four numbers first and then add

            600        592 rounds to 600
            400            421 rounds to 400
            400            389 rounds to 400
        +  800            830 rounds to 800
          2200


  2.  Application

    A space ship must travel 67,231,428 km to get to mars.  The ship can travel at 62,326 km/hr.  Estimate the total number of hour it will take the ship to travel to mars.

    Solution

    To find the number of hours, we can divide the total km by the speed.  To make this easier, we first round the two numbers

            60000 |70000000  

    We can simplify this calculation by getting rid of four zeros from both numbers:

                1166 R 4
            6 |7000  
               -6
                10
                - 6
                  40
                 -36
                    40
                   -36
                      4


    Notice that the remainder is more that half of 6.  We therefore round up to the nearest whole number.

    We conclude that it takes about 1167 hours to get to mars.

    Exercises

    Use rounding to estimate

    1. 345 + 278 + 523 + 289        1,400
    2. 74,237 - 28,153        40,000
    3. 3,512 x 2,119        8,000,000

 

Back to the Arithmetic of Whole Numbers page

Back to the Math 187A page

e-mail Questions and Suggestions