3 by 3  Linear Systems

Geometry of 3X3 systems

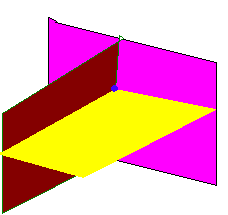
Recall that for lines, either they intersect in a point, are parallel, or are the same line.  Similarly, if we have three planes either they intersect in a point, a line, don't intersect at all, or are the same planes.  Therefore when we solve three linear equations and three unknowns, we can expect that the solution is a point, a line, no solution, or a plane.  

Elimination

Step by step rules for the elimination method for solving a three by three linear system

Example:  

        x + 2y - z  = 2                Equation 1

        2x + 2y + 2z = 12          Equation2

        x - y + 2z = 5                 Equation 3

Step 1:  Choose the most convenient variable to eliminate

    In our example any seem convenient.

Step 2:  Use any two of the equation to eliminate the variable.  Then use a different pair to eliminate the same variable.  The result is a 2 by 2 system.

Multiply equation 1 by two and subtract from equation 2:

        2x + 2y + 2z  = 12

        2x + 4y - 2z   =  4
 -                                                   

               -2y + 4z  = 8

and

Multiply equation 3 by 2 and subtract from equation 2

        2x + 2y + 2z  = 12

        2x - 2y + 4z   =  10 
-                                                   

                4y - 2z   =   2

Step 3:  Use elimination to solve the system of the two equations that you found.

        2y + 4z  = 8

        4y - 2z = 2

We multiply the second equation by 2 and add it to the first equation:

        -2y + 4z  =   8

         8y - 4z    =  4 
+                                                  

                6y    =  12

        y = 2

Re-substituting:

        -2(2) + 4z  =  8 

so that 

        4z = 12,     z = 3

Step 4:  Substitute the two values into any of the three equations the get the third value.

        x + 2(2) - (3)  =  2 

so 

        x = 1

Step 5:  Substitute all three values into the three equations to check your work.

Step 6:  Reread the question and answer it.

Exercise

Solve

        3x -2y + 5z  =  2

        4x - 7y - z  =  19

        5x - 6y + 4z  =  13

Application

Example:  

Chris invests $2,200 into three accounts that pay 6%, 8% and 9% in annual interest. He has three times as much invested at 9% as he does at 6%.  If his total interest for the year is $178, how much is invested at each rate?

 Solution:

Let 

        x = the amount in the 6% account

        y = the amount in the 8% account

        z = the amount in the 9% account

then

        x + y + z   =  2,200

        3x - z  =  0

        .06x + .08y + .09z  =  178

1. Eliminate y
   
   

2. y is already eliminated in equation 2, then take 

           third - .08(first) 

   gives

           .06x + .08y + .09z   =  178

           .08x + .08y + .08z   =  176

     -                                                           

           -.02x           + .01z   =   2 

   or 

           -2x + z = 200
   
   

3. Adding equation 2 to the result gives

                    3x - z   =   0

                   -2x + z  =   200
     +                                                     

                      x      =     200

    

           3x - z  =  0 

   gives 

           z   =   600
   
   

4.         200 + y + 600 = 2200 

   gives

           y = 1400
   
   

5. ok.
   
   

6. Chris has 200 invested in the 6% account, 1400 invested in the 8% account, and 600 invested in the 9% account.

Back to the Functions Home Page

Back to the Intermediate Algebra (Math 154) Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions