Inverses

Inverses

Example:  

The inverse of the relation

        (2,3), (4,5), (2,6), (4,6) 

is

        (3,2),  (5,4), (6,2), (6,4)

Generally we switch the roles of x and y to find the inverse.

For functions, we follow the steps below to find the inverse:

• Step 1:  Switch the x and y.

• Step 2:   Solve for y.

• Step 3:  Write in inverse notation.

Example

Find the inverse of 

        y  =  2x + 1

Solution

1. We write
    
            x = 2y + 1
   
   
   

2. We solve:  
   
           x - 1  =  2y 
   
                     x - 1
           y  =                  
                       2
   
   

3.  We write 
   
                              x - 1
           f ^-1(x)   =                   
                                2
   

Notice that the original function took x, multiplied by 2 and added 1, while the inverse function took x, subtracted 1 and divided by 2.  The inverse function does the reverse of the original function in reverse order.

Exercises

Find the inverse of

1.               x - 1
   f(x)  =                
                 x + 1
   
   

2. f(x)  =  3x³ - 2   
   
   

3. f(x)  =  3x - 4   
   
   

Graphing Inverses

To graph an inverse we imaging folding the paper across the y = x line and copy where the ink smeared in the other side.  

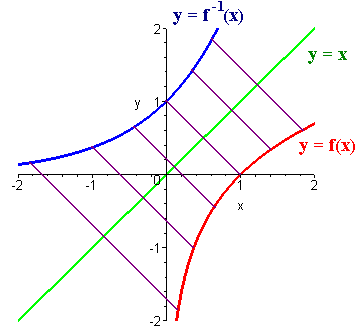
One to One Functions

A function  y = f(x) is called one to one if for every y value there is only one x value with y = f(x).  That is, each y value comes from a unique x value.

Example

1. Determine if 

           y = 2x - 3

   is one to one
   

   Solution

   For any two values a and b if 

           y = 2a - 3 

   and 

           y = 2b - 3

   then

           2a - 3  =  2b - 3

           2a  =  2b

           a  =  b

   Hence this function is 1-1.

    

    

2. Determine if 

   y  =  x²

   is one to one
   

   Solution

   Now if  

           a²   =   b²  

   then 

           a   =   b

   In particular 

           a = -b 

   is a viable solution, for example 

           1²  = (-1)²

   hence this function is not 1-1. 

The Horizontal Line Test

If the graph of a function is such that every horizontal line passes through the graph at at most one point then the function is 1-1.  

The graph below is the graph of a 1 -1 function since every horizontal line crosses the graph at most once.

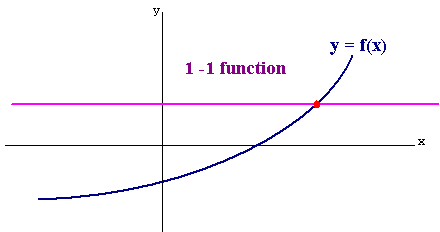
However, the graph below is not the graph of a 1 -1 function, since there is a horizontal line that crosses the graph more than once.

 

Theorem If a function is 1-1, then its inverse is also a function

An application of this is if we want a computer to find an inverse function, then we first have the computer check to see if the function is one to one, then have it proceed to find the inverse.

Back to the Functions Home Page

Back to the Intermediate Algebra (Math 154) Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions