Nonlinear Systems Relations and Functions

Relations and Functions

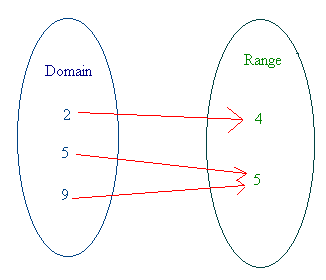
A relation is a rule that takes an input from a set (called the domain) and gives one or more outputs of another set (called the range).

Examples

(0,0), (4,4), (0,3), (2,1)
y = 2x
The circle is a relation. We can go from an x-coordinate to the y-coordinates of the circle that have that x-coordinate.

A function is a relation such that for every input there is exactly one output.

Examples:

Examples 2 and 3 above are functions, whereas examples 1 and 4 are not functions.

Determining the Domain of a Function

Rule 1: The domain of a polynomial is the set of all real numbers.

Example:

For

f(x) = 3x² + 2x - 1

the domain is the set of all real numbers.

Rule 2: The domain of a rational function (poly)/(poly) is the set of all real numbers except where the denominator is 0.

Example:

For

                          x - 1
        f(x)   =
                          x + 1

the domain is all real numbers except where x = -1.

Rule 3: The domain of a square root function is all real numbers that make the inside of the square root positive.

Example:

Find the domain of

Solution:

We set up the inequality

x² - x - 6 > 0

and use our steps of quadratic inequalities to solve. Factoring we get

(x - 3) (x + 2) > 0

Putting -2 and 3 on a number line, gives three regions. The table shows

x+2 x - 3 Total

Left (-3)
-

-

+

Middle(0)
+

-

-

Right(4)
+

+

+

Hence the solution is

(-,-2] U [3,)

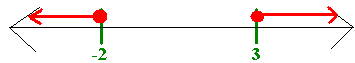
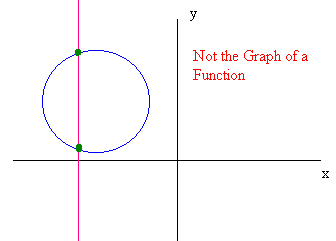
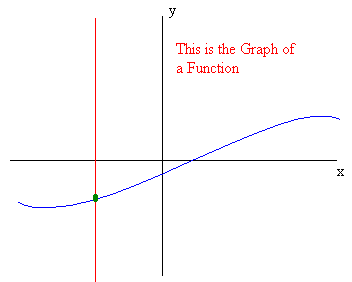
The Vertical Line Test

If every vertical line passes through the graph at most once then the graph is the graph of a function.

Example

The Circle is not the graph of a function since there are vertical lines that cross it twice.