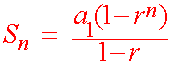Geometric Sequences and Series 

Geometric Sequences

Find the general term of the following:

1. 1, 2, 4, 8, 16, ...
   
   
   

2. 27, 9, 3, 1, 1/3, ...
   
   
   

3. 3, 6, 12, 24, 48, ...
   
   
   

4. 1/2, -1, 2, -4, 8, ...
   

 

Definition of a Geometric Sequence A Geometric Sequence is a sequence which the ratio of the common terms is equal. The general term is                     an  =  a1rn-1  where r is the common ratio.

Example

Find the general term of the geometric series such that

        a₅  =  48 

and 

        a₇  =  192

Solution

We have that 

        a_n  =  a₁rⁿ  

which gives the equations

        48  =  a₁r⁴ ,         192  =  a₁r⁶

Dividing the two equations, we get:    

        4  =  r²

Hence 

        r  =  2         or         r  =  -2

Substituting back into the first equation, we get

        48  =  16a₁

So that 

        a₁ = 3

Hence the general term of the sequence is

        a_n  =  (3)(2)^n-1          or         a_n  =  (3)(-2)^n-1  

Geometric Series

 

Theorem

Example

Find the sum

        5 + 10 + 20 + 40 + ... + 2560

Solution:     

        a₁  =  5     and     r  =  2     and     n  =  10 

so that

                     a₁(1 - rⁿ)
        S_n  =                     
                        (1 - r)

                   5(1 - 2¹⁰)                   
         =                             
                      1 - 2

        =  5115

For an infinite geometric series if  |r| <1 then

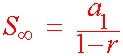
Example

How much is going to taxes?  Suppose that we track a tax refund of $100.  Each time money is spent 8% goes towards taxes and the rest gets spent again.  How much of the original $100 will go back to taxes?

Solution

        a₁ = 8       r = 0.92    (The next amount to be taxed is 92% less than the current amount)

                               a₁  
                S   =            
                              1 - r 

                          8               8
                =                 =             =  $100
                    1 - 0.92         0.08

Hence all of the refund will eventually find its way back to the government coffers.

Back to the Sequences and Series Home Page

Back to the Intermediate Algebra (Math 154) Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions