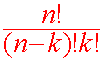Binomial Expansions

Binomial Expansions

Notice that 

        (x + y)⁰  =  1 

        (x + y)²  =  x² + 2xy + y²

        (x + y)³  =  x³ + 3x³y + 3xy² + y³  

        (x + y)⁴  =  x⁴ + 4x³y + 6x²y² + 4xy³ + y⁴  

Notice that the powers are descending in x and ascending in y.  Although FOILing is one way to solve these problems, there is a much easier way.

Pascal's Triangle

We can write the coefficients suggestively as

              1

          1     1

       1     2     1

    1    3     3     1

 1     4    6     4     1  

We see that a number is constructed by adding the two numbers above it.  The borders of this triangle are all ones.  This triangle is called Pascal's Triangle.

Exercise

What is the next row of Pascal's Triangle? 

Method of determining (x + y)ⁿ  

We use this triangle as follows.

Example

Expand

        (x + y)⁵  

Solution

1. Write the nth row of Pascal's Triangle leaving lots of space
   
              1         5         10         10         5         1
   

    

2. Start with xⁿ  and insert it next to the first term of the written row of Pascal's Triangle.   Add a "+" sign.

           1x⁵  + 5    10    10    5    1
   
   
   

3. Insert x^n-1y next to the second number of Pascal's Triangle and add a "+" sign.

           1x⁵  + 5 x⁴y + 10    10    5    1
   

    

4. Continue this process decrementing the power of x and incrementing the power of y until you place the term yⁿ  next to the final number.

           1x⁵  + 5 x⁴y + 10x³y² + 10x²y³ + 5xy⁴ + 1y⁵  
   

Exercises:  

Expand

1. (2x - y)⁴
    
   
   

2. (x - y)⁶  
   

Factorials and Pascal's Triangle

We define 

        5! = (5)(4)(3)(2)

and 

        n! = (n)(n - 1)(n - 2)....(3)(2)

 

Theorem In the expansion of (x + y)n  the coefficient in front of the term            xn-k yk    is

Example:

In the expansion (x + y)⁹ the coefficient in front of x³y⁶ is

               9!
                             
       (9 - 6)! (6!)

                9(8)(7)(6)(5)(4)(3)(2)
        =                                              
                (3)(2) (6)(5)(4)(3)(2)

                9(8)(7)
        =                      =  3(4)(7)  =  84
                (3)(2)

Exercises   

1. Find the 8th term of the  expansion of the binomial
   
                   (2x - y)¹⁴
   
    
   
   

2. Find the third term of expansion of the binomial

                   (x + 3y)¹⁰

   
   

Back to the Sequences and Series Home Page

Back to the Intermediate Algebra (Math 154) Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions