LOGARITHMS

The inverse of the exponential function-- Logarithms

Below is the graph of 

        y  =  2^x  

and its inverse which we defined as

        y   =  log₂ x

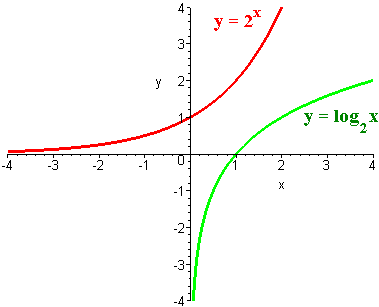
We see that the logarithm function y = log_bx has the following properties:

1. The x - intercept is (1,0).
   
   

2. There is a vertical asymptote at x = 0.
   
   

3. The domain is {x | x > 0}.
   
   

4. The range is all real numbers.
   
   

5. The graph goes through (b,1).

Evaluating Logarithms

Example

Evaluate 

        log₃ 81

Solution:  

We run the "hook" as shown below

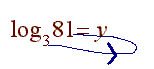
and write 

        3^y  =  81 

so that 

        y  =  4 

Exercises

Evaluate the following

1. log₁₀ 100,000,000        
   
   

2. log₅ (1/125)       
   
   

3. log₂₇ 9       

Example

Solve

        log₉ x = 2

Solution 

We write 

        x  =  9²  =  81

Exercises

Solve

1. log₂ x  =  5       
   
   
   

2. log_b 64  =  3        

Inverse Properties of Logs

Since logs and exponents cancel each other we have:

        b^{logb x} = x 

and

        log_b b^x = x

Example

    2^{log2 3} = 3

and

        log₄ 4⁵ = 5

Three Properties of Logs

        Property 1:  log_b (uv)  = log_b u  +  log_b v    (The Product to Sum Rule)

        Property 2:  log_b (u/v) = log_b u  -  log_b v    (The Quotient to Difference Rule)

         Property 3:  log_b u^r   =  rlog_b u                    (The Power Rule)

Proof of the power rule

We have the rule for exponents:

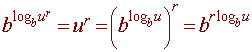
Canceling the b we get

        log_b u^r   = rlog_b u

Example

Expand:  

        log₂ (xy²/z)

by property 2 we have:

        log₂ (xy²) -  log₂ z

by property 1 we have

        log₂ x + log₂ y²  - log₂ z

By property 3 we have

        log₂ x + 2 log₂ y - log₂ z

Exercise

Try to expand:

Example

Write as a single logarithm:

        4 log₂ x - 1/2 log₂ y  + log₂ z

Solution:

We first use property 3 to write:

        log₂ x⁴ - log₂ y^1/2  + log₂ z

Now we use property 2:

        log₂ x⁴/y^1/2  +  log₂ z

Finally, we use property 3:

                   x⁴z 
        log₂ (           )  
                  y^1/2
                    

Exercise

Write the following as a single logarithm:

        1/3 log₃ x + 2 log₃ y  - 3 log₃ z

Example

Suppose that  

        log₂ 3 = 1.58 

and that 

        log₂ 5 = 2.32

Find 

        log₂ 90

Solution

Since 

        90 = (2)(5)(3²)

We have

        log₂ 90  =  log₂ (2)(5)(3²)  =  log₂ 2 + log₂ 5 + log₂ 3²

        =  1 + 2.32 + 2log₂ 3

        =  1 + 2.32 + 2(1.58)  =  6.48

Exercise

Find 

        log₂ 40/27       

Back to the Exponentials and Logs Home Page

Back to the Intermediate Algebra (Math 154) Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions