Exponentials

Graphing Exponential functions

We  graph 

        y = 2^x

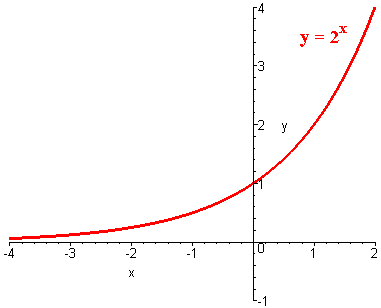
and 

        y = (1/2)^x

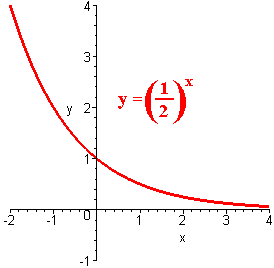
by plotting points.  

It turns out that all functions of the form 

        y = b^x  

have this shape.  

To graph y = b^x, where b>1, we plot the point (0,1) and the point (1,b) and connect the dots keeping the exponential shape.  We see that the exponential function is one to one since it passes the Horizontal Line Test.

Exercises 

Sketch the Graphs of 

1. y = 4^x  
   
   

2. y = (1/4)^x  

We will call functions of the form 

        f(x)  =  b^x  

exponential functions.

Some Algebraic Examples

Example:  

Solve

        8^x  =  4^x+1

Solution:

We can write 

        8  =  2³     and      4  =  2²

Hence

        2^3x  =  2^{2(x + 1)}

So that

        3x  =  2(x + 1)

        3x  =  x + 2

        x = 2

Exercise

Solve

Example  

Suppose that the population of the world doubles every 40 years.  If the population today is 6 billion what will it be in 15 years?

Solution

We have 

        y = 6(2)^x/40

so that after 15 years we have that

        y  =  6(2)^15/40  =  7.78 billion. 

e

The compound interest formula says that if 1 dollar is invested in an account that pays at a rate of interest of 100% compounded n times per year then the amount A in the bank after one year is

        A  =  (1 + r/n)ⁿ  

if n is large this amount is about

        2.71692

for an infinite n we call this number e.  Think of continuous compound interest, such as inflation.  In general if the rate of inflation is r then a commodity worth $P today will be worth

        A  =  Pe^rt

Dollars after t years. 

Example

If the rate of inflation holds at a steady 3% over the next hundred years, how much will a car that costs $20,000 cost in 100 years?

Solution

We have 

        r  =  0.03,    P  =  20,000,     t  =  100

So that

        A  =  20000e^(0.03)(100)  =  $401,710

or about four hundred thousand dollars!

Notice that the exponential curve general holds true for prices such as the stock market.  Below is a picture of the Dow Jones Industrial Average between 1985 and 2000.  

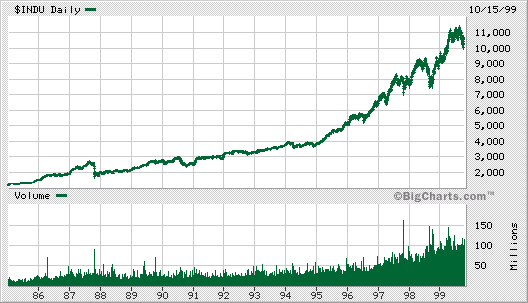
Trivia Question:  Does the exponential curve accurately predict the market value after 1999?

Back to the Exponentials and Logs Home Page

Back to the Intermediate Algebra (Math 154) Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions