Practice Exam 2
Please work out each of the given problems. Credit will be based on the steps that you show towards the final answer. Show your work.
Problem 1
Use your calculator to find log329 rounded to three decimal places.
Solution
We use the change of base formula.
log 29 1.4624
log3 x
=
=
= 3.065
log
3
0.4771
Problem 2
Solve for x: ln(x + 1) + ln(x + 2) = 3
Solution
First use the sum to product formula to write this as a single logarithm.
ln[(x + 1)(x + 2)] = 3
Now write this as an exponent
(x + 1)(x + 2) = e3
Multiply the left hand side out to get
x2 + 3x + 2 = e3
or
x2 + 3x + 2 - e3
This is a quadratic with
a = 1 b = 3 c = 2 - e3
We can use the quadratic formula to get
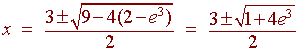
Problem 3
The number of grams N of C14 left in a fossil after t years is
N = 0.03e-.000121t
A fossil has been analyzed and found to contain 0.0002 grams. How old is the fossil?
Solution
We have
0.0002 = 0.03e-.000121t
0.0066667 = e-.000121t
Now turn this into a natural logarithm equation
-0.000121t = ln(0.0066667) = -5.01
Divide by -0.000121 to get
t = 41,410 years old
Problem 4
Write
2 logq (5x) - logq (3x - 2) as a single logarithm
Solution
First use the power rule to get
logq (5x)2 - logq (3x - 2)
= logq (25x2) - logq (3x - 2)
Next use the quotient property to get
25 x2
logq
3x - 2
Problem 5
Expand the logarithm
25 x10
log5
y12
as much as possible and simplify.
Solution
First use the quotient property of logs to get
log5(25x10) - log5(y12)
Now use the product property on the first term to get
log5(25) + log5(x10) - log5(y12)
Now use the power property and the fact that 25 = 52 so that the first term is just 2.
2 + 10 log5(x) - 12 log5(y)
Problem 6
A. Find the equation of the conic shown below
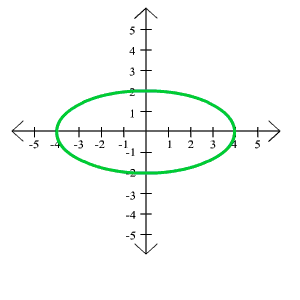
Solution
Since the vertices are at (-4,0), (4,0) and (0,-2), (0,2), the conic is an ellipse with a = 4 and b = 2. The equation is
x2
y2
+
= 1
16 4
B. Sketch the graph of the conic with the equation below:
9y2 - x2 = 36
Solution
First divide all three terms by 100 to get
y2
x2
-
= 1
4 36
Now notice that this is a hyperbola with a = 6 and b = 2. Now sketch the hyperbola. The vertices of the hyperbola are at
(0,-2) and (0,2). The helper points to complete the rectangle are at (-6,0) and (6,0). If you sketch the rectangle and use the diagonals as the asymptotes, you will get the graph shown below.
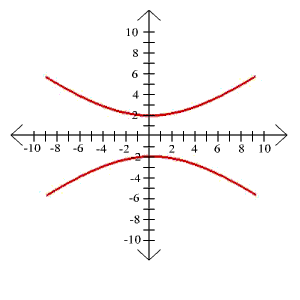
Problem 7
Solve the following nonlinear system of equations
2x2 - 3y2 = 29
x2 + y2
= 17
Solution
We can multiply the second equation by 2 to get
2x2 - 3y2 = 29
2x2 + 2y2
= 34
Now subtract the second equation from the first to get
-5y2 = -5
y2 = 1
y = -1 or y = 1
Plugging these into the second equation gives
2x2 + 2 = 34
x2 + 1 = 17
x2 = 16
x = -4 or x = 4
This gives the four points
(-4,-1), (-4,1), (4,-1) and (4,1)
Problem 8
A. Find the indicated unknown
8, 13, 18, 23, ..., 88 n = ?
Solution
This is an arithmetic sequence since
13 - 8 = 18 - 3 = 23 - 18 = 5
The common difference is d = 5.
The first term is 8, so the general formula is
an = 8 + 5(n - 1)
The last term is 88, so we set
88 = 8 + 5(n - 1)
80 = 5(n - 1) Subtract 8
16 = n - 1 divide by 5
n = 17 add 1
B. If the second term of a geometric sequence is -2/3 and the third term is 1/3, find a1 and r.
Solution
Since this is a geometric sequence, we can find r by dividing a term by its previous term. That is
1/3 1
3 1
r =
=
x =
-
-2/3
3 -2
2
Now we can find a1 by using the formula
a2 = a1 (r)1
or
-2/3 = a1(-1/2)
so that
-2/3 -2
-2 4
a1 =
=
x =
-1/2
3 1
3
Problem 9
Sketch the graph of the circle with equation
x2 + y2 + 4x - 6y = 3
We first complete the squares
x2 + 4x + 4 + y2 - 6y + 9 = 3 + 4 + 9
(x + 2)2 + (y - 3)2 = 16
Hence the center is at (-2,3) and the radius is 4. The graph is shown below.
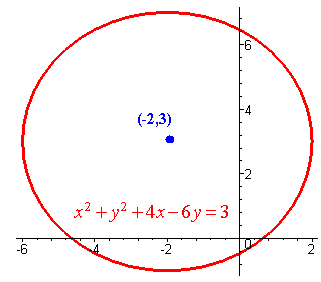
Problem 10
Find the equation of the parabola that opens downward, has vertex (1,3) and passes through the point (2,1).
Solution
The standard equation is
y = a(x - h)2 + k
Since the vertex is at (1,3) we have
y = a(x - 1)2 + 3
Since it passes through the point (2,1), we have
1 = a(2 - 1)2 + 3 = a + 3
hence
a = -2
The parabola has equation
y = -2(x - 1)2 + 3 = -2(x2 - 2x + 1) + 3
y = -2x2 + 4x + 1
Problem 11
Lake Tahoe Community College had 4200 students in 2002, and has had a enrollment decline of 150 students each year since 2002.
A. Find the enrollment for each of five years, beginning with 2002.
Solution
To find the enrollments, just subtract 150 from the previous number. The enrollments are shown below:
| Year | Enrollment |
| 2002 | 4200 |
| 2003 | 4050 |
| 2004 | 3900 |
| 2005 | 3750 |
| 2006 | 3600 |
B. Find the general term an of this sequence.
This is just an arithmetic sequence with first term 4200 and common difference -150. The general term is
an = a1 + d(n - 1) = 4200 + (-150)(n-1)
an = 4200 - 150(n - 1)