MATH 154 Practice Midterm I  Key

Please work out each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Show your work.

Problem 1   Solve the inequality.  Write the solution on a number line.

        2x² - 5x  >  3

Solution

We first bring all terms to the left hand side and factor

         2x² - 5x - 3  >  0

           (2x + 1)(x - 3)  >  0

The key points occur when the left hand side equals 0 that is

        x   =   -1/2    or    x  =  3

Cut the number line into the regions 

1. to the left of -1/2
   

2. between -1/2 and 3
   

3. to the right of 3

Now set up the table

Since the inequality is ">" we want the positive regions.  We include the endpoints -1/2 and 3.  Our solution is 

        (-, -1/2]  U  [3, )

Problem 2

A. Solve  x^1/2 + 2x^1/4 - 8  =  0  

Solution

Let    

        u  =  x^1/4         u²  =  x^1/2  

Substituting gives

        u² + 2u - 8  =  0

        (u - 2)(u + 4)  =  0

        u  =  2    or    u  =  -4

Resubstituting gives

        2  =   x^1/4     or    -4  =  x^1/4 

        (2)⁴  =  (x^1/4)⁴    or    (-4)⁴  =  (x^1/4)⁴ 

        x  =  16    or    x  =  256

Now we verify that 16 is a solution, however plugging 256 back in doe not yield 0.  Hence the only solution is x  =  16.

Problem 3  

Graph the following and label the important features:

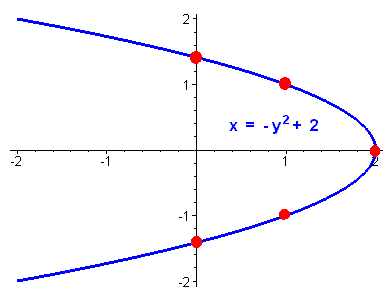
1. x = -y² + 2

Solution

First notice that this is a sideways parabola.  Now draw a T-Table:

        x  |  y
            |            
        2  | 0
        1  | 1
       -1  | 1

Notice that if x = 0 then y is   

With this information, we can sketch the graph

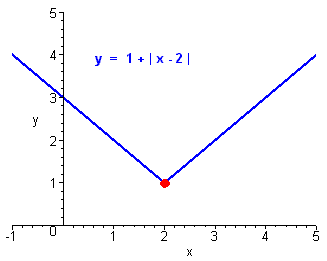
2. y  =  1 +  | x - 2 | 

Solution

This is a absolute value function, so the graph looks like a "V".  We see that the standard curve is shifted to the right by 2 and up 1.  We can now sketch the graph.

Problem 4

Answer the following True or False.  If True, explain your reasoning, if False, explain your reasoning or show a counter-example.

A.     (7 Points)  All parabolas y = ax² + bx + c are graphs of functions.

Solution

        True, since these parabolas pass the vertical line test.

B.     (7 Points)  If the vertex of the parabola y = ax² + bx + c   has positive y-coordinate and the parabola is concave up, then the parabola has two x-intercepts.

Solution

False,  it will have no x-intercepts.  For example, y  =  x² + 1 has not x intercepts.

C.     (7 Points)  If a graph has two y-intercepts then the graph is not the graph of a function.

  Solution

True, is it has two y-intercepts then there are two y values that come from the same x value.

Problem 5  Let f(x) = 3x + 2, g(x) = x + 3, and c(x) = -1.  Find

A) (5 Points)     f _° g (x)  

Solution

        f(g(x))  =  f(x + 3)  =  3(x+ 3) + 2  =  3x + 11

B) (5 Points)        f(x + h) - f(x)
                                                                  
                                    h

Solution

        f(x + h)  =  3(x + h) + 2

so

        f(x + h) - f(x)  =  3(x + h) + 2 - (3x + 2)  =  3x + 3h + 2 - 3x - 2  =  3h

Dividing by h gives

         f(x + h) - f(x)              3h
                                    =              =  3
                  h                         h

C) (5 Points)      g(f(1))     

Solution

        f(1)  =  3(1) + 2  =  5

        g(f(1))  =  g(5)  =  5 + 3  =  8

D) (5 Points)    c _° f (2)     

Solution

        f(2)  =  3(2) + 2  =  8

        c(8)  =  -1    c is always -1

E) (5 Points)           c(x)g(x)
                                                                
                             f(x) - 7c(x)

Solution

  Plugging in, we get

             (-1)(x + 3)                -x - 3            -(x + 3)                 1
                                       =                   =                        =  -             
            3x + 2 - 7(-1)            3x + 9            3(x + 3)                3

Problem 6  

Consider the function

    f(x)  =  3x - 2

A.  Sketch the graph of f(x) and explain in a complete sentence why the graph indicates that f(x) has an inverse function.

Solution

The graph is a line with slope 3 and y-intercept -2.  Below is the graph

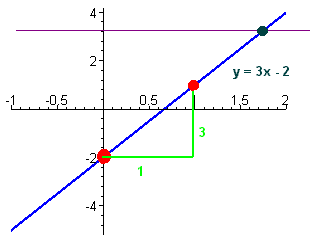
Since every horizontal line passes through the graph exactly once, the graph is the graph of a function.

B.  Find (algebraically) f ^-1 (x).

Solution

We switch and solve:

        x  =  3y - 2

        x + 2  =  3y            Add 2 to both sides

          x + 2   
                      =  y            Divide both sides by 3
             3

so that 

                       x + 2   
     f ^-1(x)  =                 
                         3

Problem 7  (16 Points)  Graph the quadratic function.  Label any intercepts, the vertex, and the axis of symmetry.

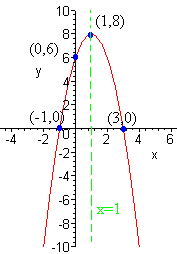
        y  =  -2x² + 4x + 6

Solution

The x-coordinate of the vertex is 

         x  =  -b/2a  =  -4/-4  =  1

Now plug 1 into the equation to get

        y  =  -2(1)² + 4(1) + 6  =  8

Hence the vertex is at (1,8).

To find the y-intercept plug in 0 for x to get

        (0,6)

To find the x-intercept, plug in 0 for y to get

        0  =  -2x² + 4x + 6

        0  =  x² - 2x - 3        Dividing by -2

        0  =  (x - 3)(x + 1)    Factoring

        x  =  3  or   x  =  -1    The zero product rule

The x-intercepts are 

        (3,0)    and    (-1,0)

Notice that the coefficient of x² is negative, so the graph is concave down. Now plot the points and sketch the graph.

Problem 8  The graphs of y = f(x) and y = g(x) are given below.  Find

A.       f(0)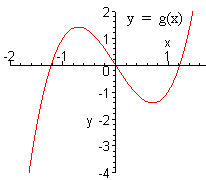

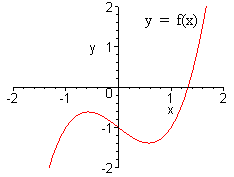
B.       g(-1)

C.    f ^-1 (1) 

D.         g _° f (1)  

E.         f(1)
                             
   g(-1)

  Solutions

A.  f(0) is the y-intercept of the graph of f(x) which is -1.

B.  g(-1)  =  1 since the graph goes through (-1,1).

C.  We are looking for the x such that y  =  1.  The graph shows that this is about 1.5.

D.  Since f(1)  =  -1, we plug -1 into g.  g(-1)  =  1.

E.  f(1)  =  -1, g(-1)  =  1.  Now divide to get -1/1  =  -1.

Extra Credit:  Write down one thing that your instructor can do to make the class better and one thing that you feel that the instructor should continue doing.

(Any constructive remarks will be worth full credit.)