Practice Exam 1

Please work out each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Show your work.

Key

Problem 1  Solve the inequality.  Write the solution on a number line.

        2x² - 5x > 3

Problem 2 

Solve  x^1/2 + 2x^1/4 - 8  =  0 

Problem 3 

Solve

Problem 4  The graph of y = x² + 2 is shown below.  Find the equation of the other parabola.

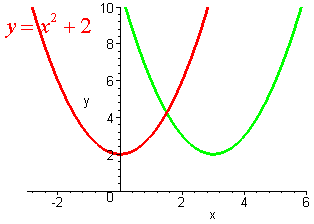
Problem 5

Find the domain and range of 

        y  =  x² + 5

Problem 6  Find the domain of

            x² - 5x - 1
                                                    
          x³ - 3x² + 2x

Problem 7

Answer the following True or False.  If True, explain your reasoning, if False, explain your reasoning or show a counter-example.

A.     (7 Points)  All parabolas y = ax² + bx + c are graphs of functions.

B.     (7 Points)  If the vertex of the parabola y = ax² + bx + c  has positive y-coordinate and the parabola is concave up, then the parabola has two x-intercepts.

C.     (7 Points)  If a graph has two y-intercepts then the graph is not the graph of a function.

Problem 8

If 

        f(x)  =  x² - x        and         g(x) = 2x + 1

find

A.  gog ^-1(x)

B.  f^.g(2)

B.  gof(3)

C.  fof(x)

Problem 9

Use the graphs to find gof(1)

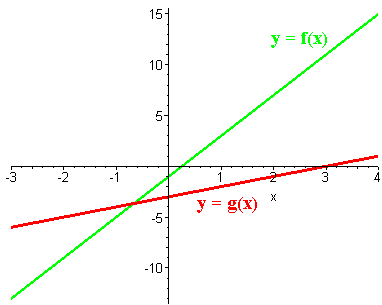
Problem 10

The graph of f(x) is shown below.  Sketch the graph of f ^-1(x).

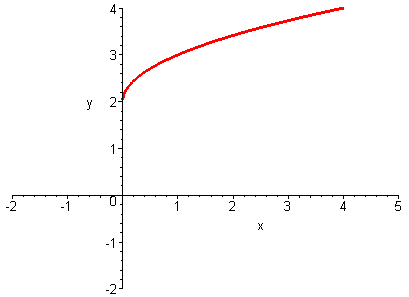
Problem 11

If the graph of f(x) = b^x passes through (2,16), find f(3).

Problem 12  Graph the quadratic function.  Label any intercepts, the vertex, and the axis of symmetry.

        y  =  -2x² + 4x + 6

Problem 13

Sketch the graph of y = 5^x.

Problem 14

Solve for w in 

        2^2w  =  1/256

Problem 15

When a certain radioactive element decays, the amount to the element A at any time t is given by

        A  =  25 (2^t/1500)

How much of the element will be left after 3000 years?

Problem 16 

One muffin, two pies, and three cakes cost $23.  One Muffin, three pies , and two cakes cost $21.  One muffin, four pies, and five cakes cost $39.  Find the cost of each.