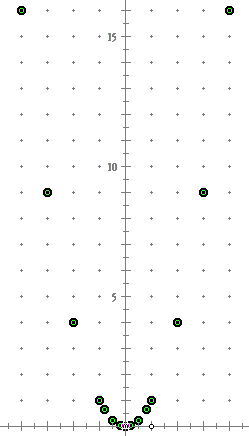
Parabolas
Consider the plot of
y = x2
to the right
The point at the bottom (or top) is called the vertex and the line that cuts the parabola into two equal pieces is called the axis of symmetry.
Example
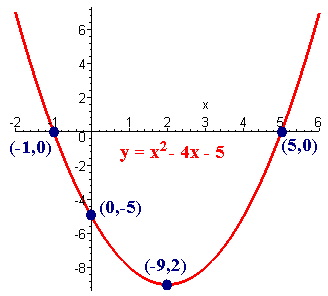
sketch the graph of the parabola
y = x2 - 4x -5
Step 1: Find the x-coordinate of the vertex- -b/2a
x = 4/2 = 2
Step 2: Find the y-coordinate of the vertex by plugging the x-coordinate into the equation.
y =
22 -4(2) - 5 = -9
Therefore the vertex has coordinates (2,-9)
Step 3: Find the y-intercept by plugging in 0 for x
y = 02 - 4(0) - 5 = -5
Step 4: Find the x-intercepts by setting y = 0 and factoring or quadratic formula.
0 = x2 - 4x - 5
(x - 5) (x + 1) = 0
x = 5 or x = -1
Step 5: If necessary, plug in more values of x to find a few additional points.
(Here it is not needed since we already have four points:
(2,-9), (0,-5), (5,0), (-1,0)
If steps 1 through 4 produce fewer than 3 points, it is recommended to plot a few additional points.
Step 6: Graph it!
Exercises
Graph
-
y = x2 - 4x - 45
-
y = 2x2 + 5x + 3
-
y = 4x2 + 8x - 21
Maximum and Minimum Problems
Example:
Suppose that you own a large piece of property along a straight part of the lakefront. You have enough money to buy 200 feet of fencing to enclose a rectangular beach. What should the dimensions of your beach be so that you have the maximum area of beach?
Solution
You only need to build the fence on three sides of the rectangle. Let x be the length of fence perpendicular to the lake and let y be the length of the fence parallel to the lake. Then
2x + y = 200
or
y = 200 - 2x.
The area of the beach is
A = xy
= (x)(200 - 2x) = -2x2 +200x
which is a concave down parabola. The vertex represents the highest point.
-200
Vx =
= 50
2(-2)
and
200 - 2(50) = 100
Hence build a beach that is 100 feet along the lake and extends 50 feet from the lake.
Back to the Intermediate Algebra (Math 154) Home Page