More Parabolas

 

Horizontal Shifting

 Consider the graphs

     y =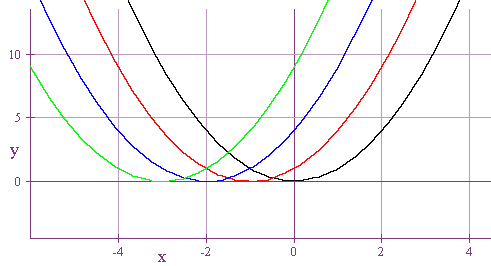 

  1. (x + 0)2

  2. (x + 1)2

  3. (x + 2)2

  4. (x + 3)3

 

We see that adding a number inside the parenthesis shifts the graph left or right.  The rules below state this precisely.

 


Rule1:  f(x - a) = f(x) shifted a units to the right.

Rule 2:  f(x + a) = f(x) shifted a units to the left

 

 

Vertical Shifting

Consider the graphs

     y  = 

  1. x3

  2. x3 + 1

  3. x3 + 2

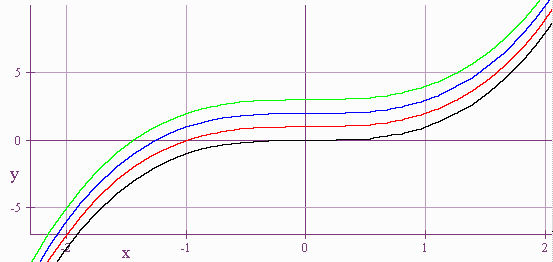
  4. x3 + 3

We see that adding a number outside the parenthesis shifts the graph up or down.  The rules below state this precisely.

 


Rule 3:  f(x) - a = f(x) shifted a units down.

Rule 4:  f(x) + a = f(x) shifted a units up.

 

 



Exercise


Use the list features of a calculator to sketch the graph of 

        y = x3  - {0,1,2,3}

 

Rule 3:  f(x ) + a = f(x) shifted a units up.

Rule 4:  f(x) - a = f(x) shifted a units down.


Reflecting About the x-axis

Consider the graphs

 y = x2  and y = -x2  

       

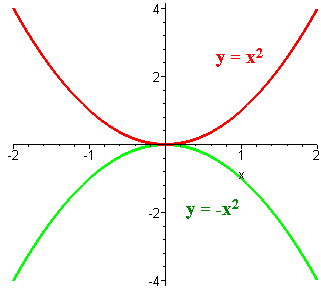
We can see that one is a reflection of the other.  This leads us to the fifth rule.

Rule 5:  -f(x ) = f(x)  reflected about the x-axis.



Reflecting About the y-axis.

Exercise: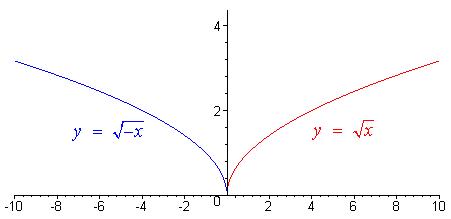

The graphs of 

          

and

       

are the same except they are reflected about the x axis.

Rule 6:  f(-x ) = f(x) reflected about the y-axis.


For an interactive investigation of the shifting rules go to 

Shifting

Back to the Conics Home Page

Back to the Intermediate Algebra (Math 154) Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions