Name
.
Math 152B
Midterm I
Please do all
of the following problems. Credit
earned will be based on the steps that you show that lead to the final solution.
Good Luck!
Problem
1: Factor the expression completely:
A)
x4 - 9x2
Solution: x2(x2 - 9)
B)
x2 + 3x - 54
Solution: (x + 9)(x - 6)
C)
6x2 + 11x - 10
Solution: AC = -60, gives (15, -4)
6x2 + 11x - 10
= 3x(2x + 5) - 2(2x + 5) = (3x - 2)(2x + 5)
D)
128xyz3 + 54x4y
Solution: 2xy(64z3 + 27x3) = 2xy(4z + 3x)(16z2 - 12xz + 9x2)
Problem
2: Perform the indicated operations and express your answer in
simplest form.
A
2x2 - x - 1 x2
- 6x + 8
.
x2 - 5x +
4 2x2 - 3x -2
(2x + 1)(x - 1)
(x - 4)(x - 2)
=
.
=
1
(x - 4)(x - 1) (2x
+ 1)(x - 2)
B
x2 + 2 xy + y2 y
+ x
![]()
x2 -
x - 2
x - 2
=
.
x2 - x - 2
=
.
=
Problem
3: Solve the following equations
A.
x3 - 2x2 + x = 0
Solution: First factor
x(x2 - 2x + 1) = 0
x (x-1)2 = 0
Now use the zero property
x = 0 or x = 1
B.
4x2 = 15 - 4x
AC = -60: (10, -6)
4x2 + 4x
= 2x(2x + 5) - 3(2x + 5) = (2x - 3)(2x + 5) = 0
2x - 3 = 0 or 2x + 5 = 0
x = 3/2 or x = -5/2
Problem
4: Solve the following inequalities
A.
|4 - 3x| < 2
Solution: 4 - 3x = 2 or 4 - 3x = -2
-3x = -2 or -3x = -6
x = 2/3 or x = 2
[2/3, 2]
B.
|3x + 1| < 0
Solution: 3x + 1 = 0, x = -1/3
Problem
5: There is a lookout
post situated in the center of a 3 mile circular trail.
How far is the lookout post from the trail?
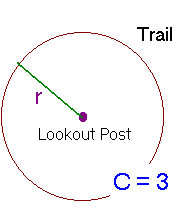
The circumference formula gives
C = 2pr where
C = the circumference (3 miles)
and
r = the radius (the distance from the lookout post to the trail)
3 = 2pr
divide by 2p
r = 3/2p
The distance from the lookout post to the trail is 3/2p miles.
Problem 6: Please answer the following true or false and explain your reasoning.
A. If all terms of a trinomial are positive, all terms of both binomial factors will be positive
Solution: True, (under the convention that the first coefficient if the first factor is always positive.)
B.
The solution to the inequality |x - 4| <
-1 is the interval [3,5].