Math 152B Practice Exam II

Please do all of the following problems.  All work and all answers must be done on your own paper.  Credit earned will be based on the steps that you show that lead to the final solution.  Good Luck!

 

Problem 1:  Find the LCD for the given rational expressions and convert each rational expression into an equivalent rational expression with the LCD as the denominator.

A.     10u                7
                       ,                                        
         39v              26u2v

Solution

First find the LCD.  The two denominators are 39v and 26u2v.  Notice that

    39  =  (13)(3)    and    26  =  (13)(2)

so for the number part of the LCD we get

    (13)(3)(2)  =  78

For the variables, we take the highest power of each:  u2v, so the LCD is

        LCD  =  78u2v

Now we build the two rational expressions so that they have the 78u2v as the denominator:

         10u         2u2              7             3
                                   ,                                                        
         39v      2u2             26u2v         3

This gives

          20u3                21
                          ,                                        
        78u2v             78u2v

 

 

 

B.        3x             5 + x
                        ,                                      
         x2 - 5x         5 - x

Solution

First factor the denominators.  For the first, we factor out the GCF and for the second, we factor out the "-" so that the x-term is positive.  The denominators become

        x(x - 5) and -(x - 5)

The LCD is

        LCD  =  x(x - 5)

Now we build the fractions so that they have the LCD as their denominators:

            3x              5 + x        -x
                         ,                                                   
         x2 - 5x         5 - x         -x

This gives

             3x             -x2 - 5x
                        ,                                           
         x2 - 5x          x2 - 5x

 

  

 

Problem 2:  Perform the indicated operations and express your answer in simplest form.

A       2x2 - x - 1     x2 - 6x + 8
                           .                                            
         x2 - 5x + 4    2x2 - 3x -2

              (2x + 1)(x - 1)     (x - 4)(x - 2)
   =                                .                               =   1                   
             (x - 4)(x - 1)        (2x + 1)(x - 2)

B       x2 + 2 xy + y2      y + x
                                                                 
          x2 - x - 2              x - 2

                  x2 + 2xy + y2      x - 2
        =                              .                                    
                   x2 - x - 2             y + x

                  (x + y)(x + y)         x - 2
        =                               .                                    
                     (x - 2)(x + 1)       x + y

                     (x + y)    
        =                                               
                      (x + 1)  

C.       x2 - x - 5                   1 - 2x
                                +                                 
         x2 +3x + 2            (x + 1)(x + 2)

Solution first notice that the first denominator factors as

        x2 + 3x + 2  =  (x + 1)(x + 2)

so that the denominators are the same.  We can add the rational expressions by adding the numerators and leaving the denominators the same.  We get

            (x2 - x - 5) + (1 - 2x)
                                                    
               (x + 1)(x + 2)

Now combine like terms to get

            x2 - 3x - 4
                                      
         (x + 1)(x + 2)

 

D.            9                      6
                              -                       
         q2 - q - 2             q2 - 1

First factor the denominators to get

        q2 - q - 2  =  (q - 2)(q + 1)     and     q2 - 1  =  (q - 1)(q + 1)

Now build the fractions to get

                   9(q - 1)                                   6(q - 2)
      =                                           -                                          
           (q - 2)(q - 1)(q + 1)            (q - 2)(q - 1)(q + 1)

 

Now multiply through to get

                   9q - 9                                     6q - 12
      =                                           -                                          
           (q - 2)(q - 1)(q + 1)            (q - 2)(q - 1)(q + 1)

now subtract the numerators

            (9q - 9)  - (6q - 12)           
      =                                         
            (q - 2)(q - 1)(q + 1)   

Remember to distribute the "-" sign through both terms on the right.

            9q - 9  - 6q + 12           
      =                                         
            (q - 2)(q - 1)(q + 1)   

Combine like terms

                     3q - 3           
      =                                         
            (q - 2)(q - 1)(q + 1)   

Factor the numerator

                     3(q - 1)           
      =                                         
            (q - 2)(q - 1)(q + 1)   

and cancel the "q - 1"s

                     3        
      =                                
            (q - 2)(q + 1)  

      

Problem 3

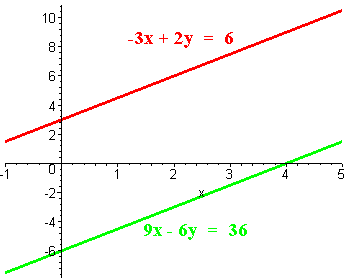
 Use the method of elimination to solve the system.  Then graph the system to check your solution.

  1.  -3x + 2y = 6
      9x - 6y  =  36

    Solution

    We multiply the first equation by 3 and add

          -9x + 6y = 18
            9x - 6y  =  36

            0  =  54

    This is a contradiction, so there is no solution.
          
    To graph it we have make T-Tables as shown below

      
    x y
    0 3
    -2 0

     
    x y
    0 -6
    4 0

    The graphs are shown below.  Notice that they are parallel.

           

     


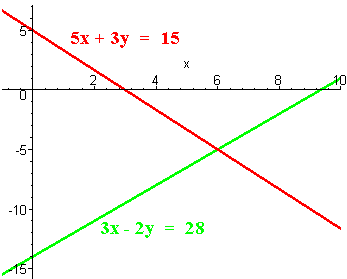
  2. 5x + 3y  =  15
    3x - 2y  =   28
     

    Solution

    Multiply the first equation by 2 and the second by 3 and add

                10x + 6y  =  30
                 9x   - 6y  =  84

                19x  =  114     
                    x  =  114/19  =  6

    Now substitute this value into the second equation (the first will work also) to get

                3(6) - 2y  =  28

                18 - 2y  =  28

                -2y  =  28 - 18  =  10

                y  =  10/-2  =  -5

    The solution is (6, -5).

    To graph it we have make T-Tables as shown below

      
    x y
    0 5
    3 0

     
    x y
    0 -14
    28/3   0

    The graphs are shown below.  Notice that the lines intersect at (6,-5).

           

     

 

  Problem 4

Use the method of substitution to solve the system.  Then graph the system to check your solution.

  1. 7x + y  =  3
    4x + 3y  =  -8
     

    Solution

    We solve the first equation for y:

            y  =  3 - 7x

    Now plug this into the second equation:

            4x + 3(3 - 7x)  =  -8

            4x + 9 - 21x  =  -8

            9 - 17x  =  -8

            -17x  =  -17

            x  =  1

    Now plug in x = 1 in the equation

            y  =  3 - 7(1)  =  -4

    Hence the solution is (1,-4).

    To graph it we have make T-Tables as shown below

     
    x y
    0 3
    3/7 0

     
    x y
    0 -8/3
    -2   0

    The graphs are shown below.  Notice that the lines intersect at (1,4).

           

     

     

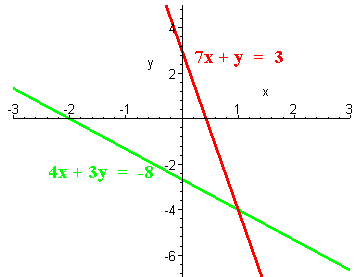
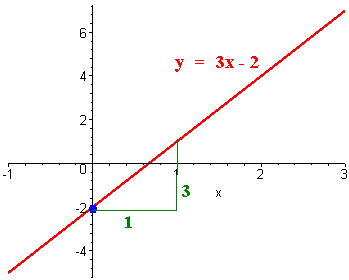
  2. y  =  3x - 2
    6x - 2y  =  4
     

    Solution

    We can substitute the first equation into the second:

            6x - 2(3x - 2)  =  4

            6x - 6x + 4  =  4

            4  =  4

    This is an identity, hence there are an infinite number of solutions (all points lying on the line y  =  3x - 2).  Notice the the y-intercept is -2 and the slope is 3.  We can draw the point (0,-2) and rise 3 and run 1 from this point to graph the line.

           

     

 

Problem 5  Solve the equation

        x - 3       x - 6
                 -               =  0
       x + 1       x + 5

Solution

        Multiple all three terms by the common denominator (x + 1)(x + 5)

        (x - 3)(x + 1)(x + 5)            (x - 6)(x + 1)(x + 5)
                                           -                                    =  0
                 x + 1                                 x + 5

        (x - 3)(x + 5)  -  (x - 6)(x + 1)  =  0

        [x2 - 3x + 5x - 15]  -  [x2 - 6x + x - 6]  =  0

        [x2 + 2x - 15]  -  [x2 - 5x  - 6]  =  0

        x2 + 2x - 15  -  x2 + 5x  + 6  =  0

        7x - 9  =  0

        7x  =  9

        x  =  9/7

 

Problem 6  Solve the following for m

                             r
        S  =  1  +            
                         m

Solution

first subtract 1 from both sides

                           r
        S - 1  =             
                       m

Now multiply both sides by m

        m(S - 1)  =  r

Now divide both sides by S - 1

                          r
        m  =                    
                    S - 1

       

Problem 7  Perla can paint her house in 10 hours working by herself.  Working together, Bill and Perla can paint the house in just 6 hours.  How long would it take Bill to paint the house by himself?

Solution

Since Perla can paint the house in 10 hours, she paints the house at the rate of 1/10 houses per hour.  If Bill can paint the house in x hours, he paints at a rate of 1/x houses per hour.  The sum of the individual rates equal the total rate (1/6 houses per hour).  

              1            1         1 
                  +          =             
          10           x          6  

Now multiply by the common denominator 30x

              1 (30x)           1(30x)        1 (30x)
                          +                 =                  
             10                   x                6  

        3x + 30  =  5x

        2x  =  30

        x  =  15

It would take Bill 15 hours to paint the house by himself.

 

Problem 8  Jason bicycled 36 miles to get to Echo Summit and back and Emma bicycled 60 miles to get to Carson Pass and back.  Emma rode 3 miles per hour faster than Jason, and her trip took an hour longer than Jason's.  What is the fastest speed that Jason could have been traveling?  (You must set up the equations, that is, no guessing).

Solution

We construct the following Distance-Rate-Time table

  Distance Rate Time
Jason 36 r t
Emma 60 r + 3 t + 1

This gives us the two equations

        36  =  rt        60  =  (r + 3)(t + 1)

The first equation gives us

        t  =  36/r

so that

        60  =  (r + 3)(36/r + 1)

Multiplying both sides by r gives

        60r  =  (r + 3)(36 + r)  =  r2 + 39r + 108

or

        r2 - 21r  + 108  =  0

        (r - 9)(r - 12)  =  0

So that

        r  =  9     or      r  =  12

The fastest that Jason could have been traveling is 12 miles per hour.

 

Problem 9  Simplify the complex fraction.  Reduce the answer to lowest terms

        1          5
              -         
       2x         x
                            
        3   -   1/x2

Solution

We first find the LCD of all of the 4 fractions.  The denominators are:

        2x,  x,  1, and x2

The number part of the LCD is 2 and the variable part is the highest power of x which is x2.  We have

        LCD  =  2x2

Now multiply all 4 terms by 2x2.

        1 (2x2)          5(2x2)
                        -                 
          2x                  x
                                             
        3 (2x2)   -    (2x2)1/x2

Now cancel to get

                x -  10x
        =                       
                6x2 - 2

We can combine the like terms on the numerator to get

                -9x
        =                    
              6x2 - 2

 

Problem 10  Statewide the ratio of student enrolled in beginning algebra who pass to those who do not pass is 3 to 4.5.  If a beginning algebra class had 24 students pass, how many would you expect not to have passed?

Solution

We use the method of ratios.  Let x be the number of students in the class who did not pass.  Then

           Pass                     3              24
                                =                 =             
        Not Pass                 4.5            x

Now cross multiply to get

        3x  =  (24)(4.5)

Now divide both sides by 3 to get

        x  =  (24)(4.5) / (3)

Notice that

        24 / 3  =  8

so we get

        x  =  (8)(4.5)  =  36

We can conclude that 36 students are not expected to pass the class.

Back to the Factoring and Rational Expressions Page

Back to the Basic Algebra Part II Page

Back to the Math Department Home Page

Questions, Comments and Suggestions  Email:  greenl@ltcc.edu