Multiplication and Division of Rational Expressions
Simplifying Rational Expressions
We define a Rational Expression as a fraction where the numerator and the denominator are polynomials in one or more variables.
Examples
x2 - y2
(x - y)2
To simplify, we just factor and cancel:
(x - y)(x + y) x + y
(x - y)2 x - y
3x2 - 4x x(3x - 4) 3x - 4
Exercises:
2x2 - x - 1

8x2 + 18x + 9

x2 - xy - 2x + 2y

Multiplication of Fractions
Recall that when we multiply fractions we first cross cancel. For example:
8 21
4 7 28
=
=
9
10 3
5 15
When we multiply rational expressions we follow the same approach. First we factor then we cross cancel.
Examples:
32a2 21x2b4
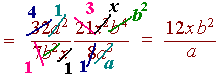
-
x2 - 2x + 1 x2 + 4x + 3
(x - 1)2 (x + 3)(x + 1)
=
= (x - 1)(x + 3)
Exercises
Multiply and simplify
14x2 9y
21x3y3 8x

2x2 - 5x - 12 3x2 -14x - 5

9x2 - 6xy + y2 6x3y
![]()
Division of Fractions
Recall that when we divide fractions we multiply by the reciprocal.
For example:
8
=
=
=
10
9
10
3
5 15
21
For rational functions we do the same thing. To divide rational functions, multiply by the reciprocal and then factor and cross cancel.
Example
17a2b3
9xy
x2 - x - 2
3x + 9
(x - 2)(x + 1) 3(x + 3) 3x - 6
=
Exercises
Divide.
17a2b3
9xy
32x2c
34b2c 9a

8x + 4
2x2 - 5x - 3

x2 - 3x - 18
x2 - 4

Back to the Factoring and Rational Expressions Page
Back to the Basic Algebra Part II Page
Back to the Math Department Home Page
e-mail Questions and Suggestions