Problem Solving and Solving Roots
Work Problems
Example
Suppose that George can finish his homework in 5 hours and Carmen can finish her homework in 4 hours. How many hours will it take for them to finish their homework if they do it together?
Solution
We can think of this problem as a distance-rate-time problem where the distance for the whole test is 1. To find George's rate we write:
d = rt
1 = (r)(5) or r = 1/5
To find Carmen's rate, write
1 = (r)(4) or r = 1/4
Hence the total rate is
George's rate + Carmen's rate = 1/5 + 1/4
This is the amount of homework done in 1 hour. If together it takes x hours to do the homework then they will complete 1/x of the homework in 1 hour.
1
1 1
+
=
5
4 x
1
1
1
(20x) + (20x)
=
(20x)
5
4
x
4x + 5x = 20
9x = 20
x = 20/9 = 2 2/9
It takes 2 2/9 hours for them to finish their homework together.
Example
A boat travels 10 mi/hr in still water. If the boat takes the same amount of time to travel 3 miles upstream as 2 miles downstream, find the speed of the current.
Let
x = speed of the current.
then the rate upstream is
Rate Upstream = 10 - x
and the rate downstream is
Rate Downstream = 10 + x
since
d = rt
t = d/r Divide both sides by r
For the two trips, the time is the same, so
3
2
=
10 +
x
10 - x
Cross multiply:
3(10 - x) = 2(10 + x)
30 - 3x = 20 + 2x
10 = 5x
x = 2.
The current is going at 2 miles per hour.
Finding Roots
|
Definition of the nth root of x We define the nth root of x
to be y if
|
Examples
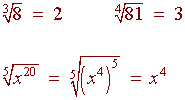
What is the solution to
y2 = -3 ?
Since the square of any number is positive, the above equation has no real solution. In general negative numbers do not have even roots.
Back to the Exponents and Radicals Page
Back to the Basic Algebra Part II Page
Back to the Math Department Home Page
e-mail Questions and Suggestions