Practice Final
Please work out each of the given problems. Credit will be based on the steps that you show towards the final answer. Show your work.
Problem 1
- If f(x) = 4 - kx, and if f(-2) = -10, find k.
Solution
f(-2) = -10 means that when x = -2, the function has value -10. We can write
-10 = 4 - k(-2)
Two negatives make a positive so we have
-10 = 4 + 2k
Subtract 4 from both sides to get
-14 = 2k
Divide both sides by 2 to get
k = -7
- Let S = {-1, 2, 4, 5, 7} and
T = {2, 3, 4, 5}. Find
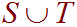
![]() means
the union of S and T,
that is a number is included if it is in either S
or T or both. These numbers are
means
the union of S and T,
that is a number is included if it is in either S
or T or both. These numbers are
{-1, 2, 3, 4, 5, 7}
Problem 2
- Evaluate the following:
[-3-2(1-(-4)) + 5] / 4
Solution
We do one operation at a time remembering our order of operations:
[-3-2(1-(-4)) + 5] / 4
= [-3-2(5) + 5] / 4 1 - (-4) = 1 + 4 = 5
= [-3 - 10 + 5] / 4 2(5) = 10
= [-13 + 5] / 4 -3 - 10 = -13
= [-8] / 4 -13 + 5 = -8
= -2
- Which property of the real numbers justifies the equality below:
x(3+y) = (x)(3) + xy
Solution
The x is being multiplied through. This is called the "Distributive Property of Real Numbers."
Problem 3
- Evaluate 3x3 - 2xy + x - 3y + 2 when x = 1 and y = -2.
Solution
We plug in
3(1)3 - 2(1)(-2) + (1) - 3(-2) + 2
= 3(1) - 2(-2) + 1 - (-6) + 2
= 3 +
4 + 1 + 6 + 2 = 16
- Simplify: 3(q - 4) - 4(2 - 5q)
Solution
We multiply through to get
= 3q - 12 - (8 - 20q)
= 3q - 12 - 8 + 20q
= 23q - 20
Problem 4
If the equation is an identity or contradiction, state so. Otherwise solve for x.
1
2
A.
(x - 3) =
(x + 1)
3
5
Solution
First multiply both sides by the common denominator (15) to get
1
2
15
(x - 3) = 15
(x + 1)
3
5
5(x - 3) = 6(x + 1) Multiply through
5x - 15 = 6x + 6 Subtract 6x from both sides
-x - 15 = 6 Add 15 to both sides
-x = 21 Multiply both sides by -1
x = -21
B. 5(3 - 2x) = 2(4 - 5x)
Solution
First we multiply through to get
15 - 10x = 8 - 10x Add 10x to both sides
15 = 8
This is a contradiction hence there is no solution.
Problem 5
When you arrived in Lake Tahoe five years ago, your math instructor had been teaching twice as long as your English instructor. Today, the total number of years that your math and English instructor have been teaching is 18 years. When did your math instructor begin teaching?
Solution
Let
x = the number of years your math instructor has been teaching
Then
18 - x = the number of years your English instructor has been teaching
and five years ago your math instructor had been teaching x - 5 years and your English instructor had been teaching 18 - x - 5 years. Hence
x - 5 = 2(18 - x - 5)
x - 5 = 36 - 2x - 10 = 26 - 2x
3x - 5 = 26
3x = 31
x = 10 1/3
Your math instructor has been teaching for 10 1/3 years.
Problem 6
Solve for x. Write your solution on a number line.
- 10 - 3x < 2
Solution
First subtract 10 from both sides
-3x < -8
Divide both sides by -3 remembering to switch the inequality sign since -3 is negative.
8
x >
= 2 2/3
3
Now place this on a number line. We use an open circle since we do not want to include the endpoint of 2 2/3.
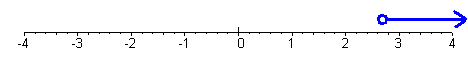
- -5 < 3 + 2x < 7
Solution
We subtract 3 from all three sides.
-8 < 2x < 4
-4 < x < 2
Now place this on a number line. We use an open circle for the excluded left endpoint, -4 and a closed circle for the included right endpoint 2.
![]()
Problem 7
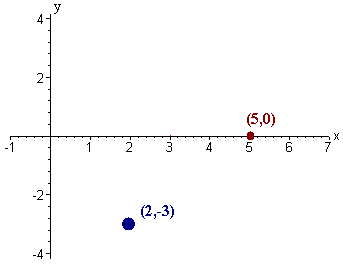
- Plot the points (2,-3) and (5,0).
Solution
We move 2 to the right and 3
down for the first point. For the second point move 5
to the right and plot this point which is on the x-axis. The points are
shown below.
- Find the slope of the line perpendicular to the line that contains the points (-2,7) and (-5,1).
Solution
First we find the slope of the line that contains the points (-2,7) and (-5,1). We use the rise over run property.
1 - 7
m =
-5 - (-2)
-6
2
=
=
-3
1
Our line is perpendicular to this line so the slope is the negative reciprocal which is
1
m = -
2
Problem 8
Graph the following lines.
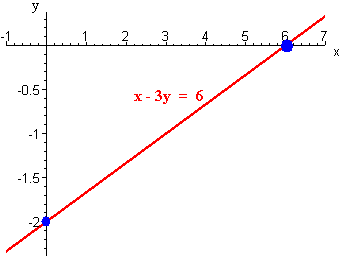
- x - 3y = 6
Solution
First construct a table. Notice that if x = 0 then
0 - 3y = 6
-3y = 6
y = -2
and if y = 0 then
x - 3(0) = 6
x = 6
| x | y |
| 0 | -2 |
| 6 | 0 |
The line passes through the points (0,-2) and (6,0). We plot these two points and connect the dots with a line.
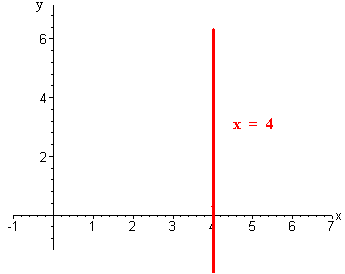
- x = 4
Solution
When there is no y in the equation, we get a vertical line. Its x-intercept is (4,0). The graph is shown below.
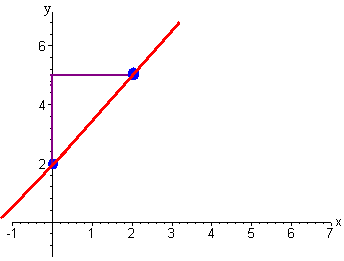
- The line with y-intercept 2 and slope 3/2.
We first draw the point (0,2). Then from this point rise up 3 and run to the right 2. Then connect the dots. The graph is shown below.
Problem 9
- Find the equation of the line that passes through the points (2,3) and (-4,1).
Solution
First, find the slope:
1 -
3
-2 1
m
=
=
=
-4 -
2
-6 3
Now use the point slope formula
1
y - 1 =
(x + 4)
Multiply through
3
1 4
y - 1 =
x +
Subtract 1 from both sides
3 3
1 4
y =
x + +
1 Note that 1
= 3/3 and add
3 3
1 7
y =
x +
3 3
- Find the equation of the line that is perpendicular to the line y = 3x - 4 and has y-intercept 4.
Solution
The given line has slope 3. To find the slope of the perpendicular line we take negative the reciprocal -1/3. Now use the slope-intercept equation of a line.
1
y = -
x + 4
3
Problem 10
Divide
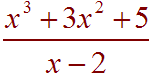
Solution
Since there are two terms in the denominator, we need to use polynomial division. Notice that the numerator does not have an "x" term. It is helpful to insert a "0x". We have

Thus the solution is
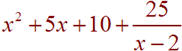
Problem 11
Find
- x(x2)3
Solution
First use the power rule for exponents.
x(x2)3 = x(x6)
Now use the product to sum rule.
x(x6) = x1(x6) = x7
- 35x2y
(32xy3)2
First use the power rule on the denominator. We can distribute the 2 through each of the powers.
35x2y=
34x2y6
Now use the division to difference rule of exponents and subtract the terms
31x0=
y5
Anything to the zero power is 1 so
3=
y5
- 4x0-3y0
Solution
Anything to the zero power is 1, hence we get
= 4 - 3 = 1
Problem 12
- What is the degree of the polynomial
x2y + xy - y2 + 7
Solution
The degrees of each of the monomial terms are
2 + 1, 1 + 1, 2, and 0
The degree of the polynomial is the highest degree of its terms, hence the
degree is 3.
- Find (3a2b3 + 2ab2 -4ab3) - (ab2 - 2a3b + 3ab3)
Solution
First distribute the "-" through
= 3a2b3 + 2ab2 - 4ab3 - ab2 + 2a3b - 3ab3
Now combine like terms
=
3a2b3 + ab2
- 7ab3 + 2a3b
- Find 3xy2(4 - x - xy2)
Solution
Just distribute
= 12xy2 - 3x2y2 - 3x2y4
Since there are no like terms, we are finished.
- Find 2xy -
x3
xy2
Solution
We can split the numerator
2xy
x3
=
-
xy2
xy2
Now we can divide using the quotient to difference rule for exponents.
2
x2
=
-
y y2
Problem 13
Find
- (2x - y)(x + 3y)
Solution
We use FOIL:
F = 2x2 O = 6xy I = -xy L = -3y2
Hence, the product is
2x2 + 6xy - xy - 3y2
Now combine like terms to get
2x2 + 5xy - 3y2
- (x - y - z)(x + z)
Solution
We distribute
(x - y - z)(x) + (x - y - z)(z)
Now distribute again to get
x2 - xy - xz + xz - yz - z2
Now combine like terms to get
x2
- xy - yz - z2
- (4x - 5y)2
We use the special product formula
(4x)2 - 2(4x)(5y) + (5y)2
= 16x2 - 40xy + 25y2
Problem 14
Solve the following equations
- |2- 3x| - 5 = 0
Solution
First add 5 to both sides to isolate the absolute value sign.
|2 - 3x| = 5
Next write this as a compound inequality.
2 - 3x = 5 or 2 - 3x = -5
Subtract 2 from both sides on each.
-3x = 3or -3x = -7
Finally divide both sides by -3 to get
x
= -1 orx = 7/3
- |3x + 4| + 7 = 0
Solution
First subtract 7 from both sides to isolate the absolute value sign.
|3x + 4| = -7
Since an absolute value can never be negative, this has no solution.
Problem 15
Write down the definition of a function
Solution
A function is a rule that assigns to each element of a set (called the domain) a unique element of a second set (called the range).
Problem 16
A beaker contain 10 ml of a 60% solution of hydrochloric acid (HCL). A chemist wants to add an amount of 25% hydrochloric acid so that the mixture is 30% hydrochloric acid. How many ml of the 25% solution should the chemist add?
Solution
Let
x = the amount of 25% hydrochloric acid that is added
Create a table containing the information.
| ml X Concentration = Amount of HCL | |||
| 25% Solution | x | 0.25 | 0.25x |
| 60% Solution | 10 | 0.60 | 6 |
| 30% Solution | 10 + x | 0.30 | 0.30(10+x) |
Since the amount of HCL from the mixture is equal to the amount from the 25% solution plus the amount from the 60% solution, we have the equation
0.25x + 6 = 0.30(10 + x)
Multiply through by 100 to get rid of the decimal.
25x + 600 = 30(10 + x)
Distribute the 30 through
25x + 600 = 300 + 30x
Subtract 30x from both sides to get
-5x + 600 = 300
Subtract 600 from both sides to get
-5x = -300
Divide both sides by -5 to get
x = 60
We can conclude that the chemist needs to add 60 ml of the 25% solution.