Practice Exam 2
Please work out each of the given problems. Credit will be based on the steps that you show towards the final answer. Show your work.
Problem 1
The number of people y in town who will buy a Lake Tahoe sweatshirt if it is offered at x dollars can be modeled by the equation
50x + y = 2000
A. Find the y-intercept and interpret this number in the context of sweatshirt purchases.
Solution
To find the x-intercept, set y equal to zero and solve for x:
50x + 0 = 2000
50x = 2000
Now divide both sides by 50 to get
x = 40
We can interpret this by saying that when the price reaches $40 no (0) Tahoe residents will buy the sweatshirt.
C. Find the slope and interpret this number in the context of sweatshirt purchases.
Solution
We put the equation into y intercept form by subtracting 50x from both sides:
y = -50x + 2000
Now, we can read off the slope as
m = -50 = -50/1
We can interpret this by saying that for every $1 increase in the price, there will be 50 fewer sweatshirts sold. (as x increases by 1, y decreases by 50)
Problem 2
Find the domain and range of each relation. Then determine whether it is a function.
A. {(1,2), (2,4), (4,7), (4,8)}
Solution
The domain is the x-coordinates: {1,2,4}
The range is the y-coordinates: {2,4,7,8}
B. x + 6y = 12
Solution
This is a line that is neither vertical nor horizontal. Hence the domain and the range are both all real numbers.
C. 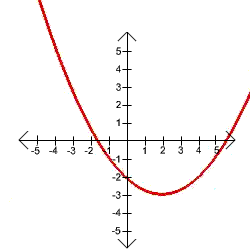
Solution
By reading the graph, we see that all x-values are obtained on the graph, hence the domain is all real numbers.
The range is the set of y-values that are achieved. Notice that the graph does not go below y = -3, but goes upward without bound. Hence the range is the set of real numbers from -3 to infinity.
Problem 3
A. If f(x) = x2 - 2x + 1, find f(-3).
Solution
To find f(-3) we just plug in -3 for x:
f(-3) = (-3)2 - 2(-3) + 1 = 9 + 6 + 1 = 16
B. If the graph of g(x) is shown in problem 2C, find g(4).
g(4) is just the y-value when x is four. You can go to the graph and see if you move to the right by 4, you must move downward 2. That is
g(4) = -2
Problem 4
Sketch the graphs of the following lines and find the x and y intercepts is they exist.
A. 2x - 5y = 10
Solution
We find set x = 0 and find y:
2(0) - 5y = 10
-5y = 10 Divide both sides by -5
y = -2
Next set y = 0 and find x
2x - 5(0) = 10
2x = 10
x = 5
This gives the table
| x | y |
| 0 | -2 |
| 5 | 0 |
The plot the points and connect with a line. The x-intercept is 5 and the y-intercept is -2. The graph is shown below.
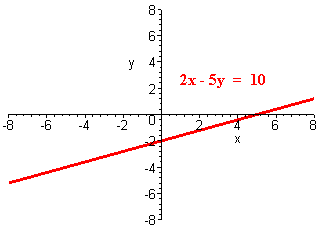
B. y = 4
Solution
This is just the horizontal line four units above the x-axis. There is no x-intercept and the y-intercept is 4.
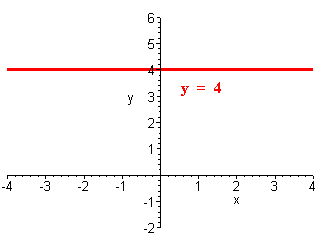
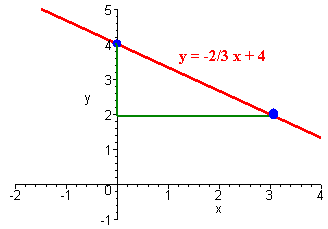
C. y + 2/3 x = 4
Solution
We can subtract the 2/3 x from both sides to get
y = -2/3 x + 4
which is a line with slope -2/3 and y-intercept 4. We can begin at the point (0,4), "rise" down 2 and "run" across 3. To find the x-intercept, set y = 0 and solve.
0 = -2/3 x + 4
0 = -2x + 12
2x = 12
x = 6
The x-intercept is 6.
The graph is shown below.
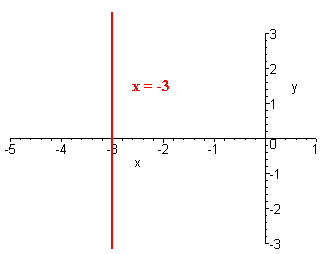
D. x = -3
Solution
This is the vertical line that crosses the x-axis at x = -3. The x-intercept is -3 and there is no y-intercept. The graph is shown below.
E. The line that passes through the point (2,4) and has slope -3/2.
Solution
We just sketch the point (2,4) then "rise" down 3 and "run" across 2. The graph is shown below.
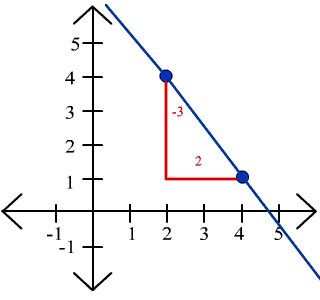
To find the intercepts, first find the equations using the point-slope formula.
(y - 4) = -3/2(x - 2)
y - 4 = -3/2 x + 3
y = -3/2 x + 7
We see that the y-intercept is 7. For the x-intercept, set y = 0 and solve.
0 = -3/2 x + 7
0 = -3x + 14
3x = 14
x = 14/3
So the x-intercept is at x = 14/3.
Problem 5
A. Find the slope of the line that is parallel to the line that passes through the points (2,-3) and (5,6).
Solution
Parallel lines have the same slope, so we need only to find the slope through the points (2,-3) and (5,6).
The rise is:
6 - (-3) = 6 + 3 = 9
and the run is:
5 - 2 = 3
Hence the slope is
m = rise/run = 9/3 = 3
B. Find the slope of the line that is perpendicular to the line that passes through the points (0,2) and (2,3).
Solution
First, we find the slope of the line through the two points.
The rise is:
3 - 2 = 1
and the run is:
2 - 0 = 2
Hence the slope is
m = rise/run = 1/2
Our line is perpendicular, so we take the reciprocal of the this slope and multiply by (-1) to get
(-1) (2/1) = -2
Problem 6
Find the equation of the line in slope intercept form with the following properties.
A. Passes through the points (2,3) and (4,-1).
Solution
First we find the slope. The rise is
-1 - 3 = -4
and the run is
4 - 2 = 2
Hence the slope is
m = rise/run = -4/2 = -2
Now use the point slope formula with the point (2,3) and the slope -2 to get
y - 3 = (-2)(x - 2) = -2x + 4 Add 3 to both sides
y = -2x + 7
B. Passes through the point (-4,2) and has slope -2/5.
Solution
We use the point slope formula to get
y - 2 = (-2/5)(x - (-4)) =((-2/5)(x + 4) = -2/5 x - 8/5 Add 2 to both sides
y = -2/5 x - 8/5 + 2 = -2/5 x - 8/5 + 10/5 = -2/5 x + 2/5
or
y = -2/5 x + 2/5
Problem 7
The graphs of several lines are shown below. decide which of the statements are true and which are false and explain your reasoning.
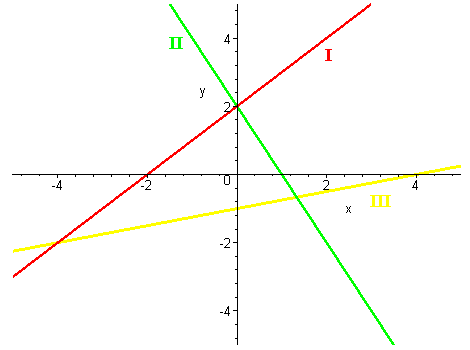
A. The slope of line II is greater than the slope of line I.
Solution
False. The slope of line II is negative and the slope of line I is positive. Negative numbers are always smaller than positive numbers.
B. The y-intercept of lines I and II are equal.
Solution
True. They are both equal to 2.
C. The x-coordinate of the x-intercept of line I is greater than the x-coordinate of the x intercept of line III.
Solution
False. Line I has negative x-intercept and line III has negative x-intercept.
D. Lines I and II are perpendicular.
Solution
False. The slope of line I is 2/2 = 1 and the slope of line II is -2/1 = -2. Since their produce is
(1)(-2) = -2
which is not -1 they are not perpendicular.
Problem 8
Simplify the expressions below.
A.
p3y4
p2y
Solution
We use the division rule of exponents. That means we subtract the exponents to get
py3
B. 51 - (xyz)0 + 30
Solution
Recall that any number to the 1 is itself and any number except 0 to the 0 power is 1. This gives
5 - 1 + 1 = 5
C . (-2x2yz3)3
Solution
Use the power rule for exponents
-8x6y3z9
Problem 9
Find
A. (x3yz - 3z3 + 2yz2 + x) + (2x3yz + 5z3 - 4x) - (2z3 - 5yz2 + x)
Solution
We add the polynomials remembering to multiply the minus sign through.
x3yz - 3z3 + 2yz2 + x + 2x3yz + 5z3 - 4x - 2z3 + 5yz2 - x
Now combine like terms
3x3yz + 7yz2 - 4x
B. 5a2b(2ab2 - a3b + 3a7b5)
Solution
Multiply the monomial by the polynomial remember to add the exponents.
10a3b3 - 5a5b2 + 15a9b6
Problem 10
A. (3x - 4)(7x + 2)
We FOIL:
F = 21x2 O = 6x I = -28x L = -8
Now add to get
21x2 + 6x - 28x - 8
Now combine like terms
21x2 - 22x - 8
B. (x2 + 2x)(3x3 - 4x + 5)
Just distribute both of the first terms into each of the three last terms to get
3x5 - 4x3 + 5x2 + 6x4 - 8x2 + 10x
Now combine like terms
3x5 + 6x4 - 4x3 - 3x2 + 10x
C. (x - 2y)(x + 2y)
Solution
This is just a difference of squares with a = x and b = 2y. We get
x2 - (2y)2
= x2 - 4y2
D. (4x + 3y)2
Solution
This is just a square of a sum with a = 4x and b = 3y. We get
(4x)2 + (2)(4x)(3y) + (3y)2
= 16x2 + 24xy + 9y2
e-mail Questions and Suggestions