Practice Exam III
Problem 1 Let C = { x|x is an even integer}, D = {2,3,5,10} and E = {1,2,3,4}
A. Find ![]()
B. Find ![]()
Solution
A. The intersection of two sets is the elements (numbers) that are included in both of the sets. The intersection is:
![]()
B. The union of two sets is the elements (numbers) that are included in at least one of the sets. The Union is:
![]()
Problem 2 The department store is having a sale on apparel. The regular price of a new dress is $48.00 and the sale price is $33.60. Find the percent discount.
Solution
Let x be the discount (given as a decimal)
Then the regular price minus the discount times the regular price equals the sales price.
48.00 - 48.00x = 33.60
-48.00 -48.00
-48.00x = -14.40
Now divide both sides of the equation by -48.00 to get
x = 0.3
we can conclude that the store is having a 30% sale on apparel.
Problem 3 Find the domain of the function
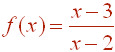
Solution
The domain is the set of all numbers x such that when we plug x in the function produces a number. This function is a fraction of linear expressions, so the only possible issue is that we may be dividing by 0. The denominator is 0 when x is 2. Therefore the domain is the set of all real numbers not equal to 2 or
![]()
Problem 4 Divide
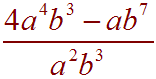
Solution
First break apart the numerator to write the expression as two fractions:
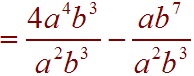
Now use the rule of exponents that says that to divide exponents, subtract the powers. Also notice that the b3 factors cancel in the first term.
![]()
![]()
Now write without negative exponents by bringing the factor with a negative exponent to the denominator with a positive exponent.
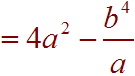
Problem 5 Divide
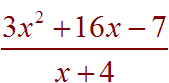
Solution
Use polynomial division
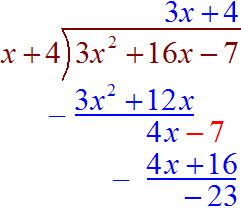
So the solution is
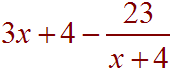
Problem 6 Divide
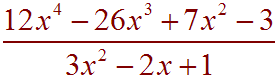
Solution
Use polynomial division
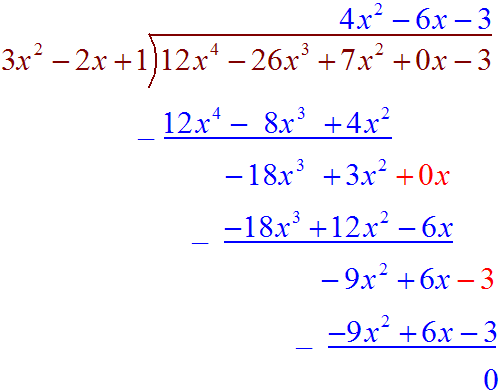
![]()
Problem 7
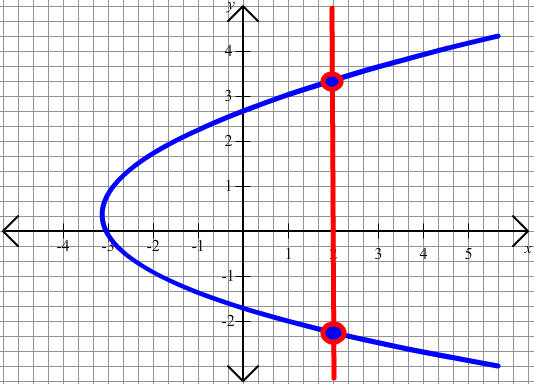
Determine whether each graph is the graph of a function.
A.
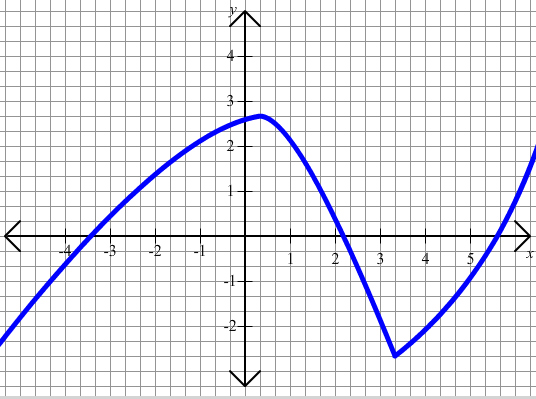
Solution
If you draw vertical lines you will notice that no vertical line crosses the graph more than once. By the vertical line test, this is the graph of a function.
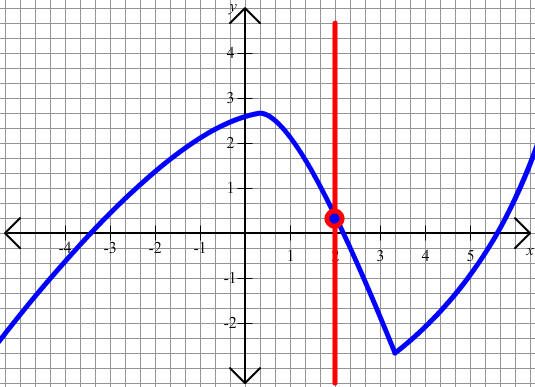
B.
We can draw a vertical line that crosses this graph twice. Hence, this is not the graph of a function of y in terms of x.
Problem 8 Tahoe Smoothie Swirl has a new drink that is 40% carrot juice. How ounces of pure carrot juice need to be added to 12 ounces of a mixed drink that is 30% carrot juice?
Solution First label the variable:
Let
x = ounces of pure juice that needs to be added
Since there are 12 ounces of the 30% mixed drink and x ounces of the pure juice,
12 + x = ounces of the 40% final drink
We can set up the table
| (Ounces) (Percent Carrot) = Total Carrot | |||
| 30% Mixed Drink | 12 | 0.30 | 3.6 |
| Pure Carrot Juice | x | 1.00 | x |
| Final Mixture | 12 + x | 0.40 | (12 + x)(0.40) |
We know that the amount of carrot juice from the 30% mixture plus the amount of pure carrot juice equal the amount in the final drink.
3.6 + 10x = (12 + x)(0.40)
Multiply through by 10 to clear the decimals
36 + 10x = (12 + x)(4)
Distribute the 4 through the right hand side of the equation to get
36 + 10x = 48 + 4x
-36 - 4x -36 - 4x
6x = 12
Divide both sides by 6 to get
x = 2
We must add 2 ounces of pure carrot juice.Problem 9 Solve each compound inequality. Write the solution set using interval notation and graph it.
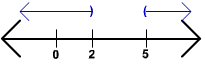
A. x - 4 > 1 or 7 - x > 5
Solution
We add 4 to both sides of the first inequality and -7 to both sides of the second.
x > 5 or -x > -2
Now multiply both sides of the second inequality, remembering to switch the inequality sign
x > 5 or x < 2
In interval notation we get
(-
![]() , 2)
U (5,
, 2)
U (5,
![]() )
)
Now put this on a number line
B. 2/3 x < 4 and x - 5 > 4
Solution
Multiply the both sides of the first by 3/2 and add 5 to both sides of the second to get
x < 6 and x > 9
Notice that these cannot happen simultaneously, so the solution is the empty set.
C. ![]()
Solution
First note that the least common denominator is 6. We multiply all three sides by this common denominator.
![]()
This gives us
-2 < 2x - 1 < 3
Now add 1 to all three sides.
-1 < 2x < 4
finally divide all three terms by 2.
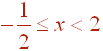
The graph is this is shown below.
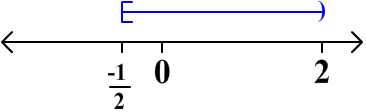
Problem 10 Solve the absolute value equation
A. 3|2 - x| + 5 = 14
Solution
First subtract 5 from both sides to get
3|2 - x| = 9
Then divide both sides by 3 to get
|2 - x| = 3
Now turn it into an or statement to find
2 - x = 3 or 2 - x = -3
Subtract 2 from both sides to get
-x = 1 or -x = -5
Now multiply both sides by -1 to get
x = -1 or x = 5
B. 5|6 - x| +7 = 3
Solution
First subtract 7 from both sides to get
5|6 - x| > -4
Then divide both sides by 5 to get
|6 - x| > -4/3
Now notice that the right hand side is negative. The absolute value can never be negative, so there is no solution.
Problem 11 Find the domain and range of each relation. Then determine whether it is a function.
A. {(1,2), (2,4), (4,7), (4,8)}
Solution
The domain is the set of first coordinates:
{1,2,4}
and the range is the set of second coordinates:
{2,4,7,8}
Since the number 4 gets sent to both 7 and 8, this is not a function.
B. x + 6y = 12
Solution
This is the equation of a line. Notice that the slope is defined:
6y = -x + 12
y = -1/6 x + 2
Since this is a line that is neither vertical nor horizontal, the graph comes from negative infinity on the left and goes to infinity on the right. Therefore, the domain is all real numbers. The graph goes from negative infinity from below and goes up towards infinity. Therefore the range is all real numbers also.
Since the slope is defined, the line is not vertical, hence the graph passes the vertical line test, and the equation is a function.
C. 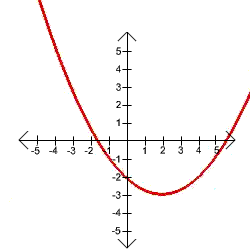
Solution
The domain is all real numbers since it comes from the far left and goes to the far right without a gap. The lowest the graph goes is -3. It is unbounded from above. Hence the range is all numbers from -3 to infinity. This graph passes the Vertical Line Test, since every vertical line passes through the graph at most once, hence it is the graph of a function.
Problem 12 Let
f(x) = 3x - 5 and g(x) = x2 - x
Find
A. f(-4)
Solution
This notation means plug -4 in for x. We get
f(-4) = 3(-4) - 5
= -17
B. f(1) - g(-3)
Solution
Plug in 1into the f equation and -3 into the g equation to get
f(1) - g(-3) = [3(1) - 5] - [(-3)2 - (-3)]
= [3 - 5] - [9+3]
= -2 - 12
= -14