Graphing Inequalities
Definition of a Linear Inequality
|
Definition A linear inequality is an inequality that has one of the four forms below
|
We follow the follow the procedure listed below to graph the inequality:
Solving Linear Inequalities
Steps for solving Inequalities
-
Write a T-table plotting the x and y intercepts (find where x = 0 and where y = 0). If the equation gives (0,0) as a point, plot another convenient point such as when x = 1.
-
Plot the two points on the xy-plane.
-
If the inequality is "<" or ">" then connect the two points with a dotted line. The dotted line is analogous to the open circle on the number line. Otherwise, connect the two points with a solid line. The solid line is analogous to the closed disk on the number line.
-
If (0,0) is not on the line, substitute (0,0) into the inequality to see if it is true for (0,0). If it is true, shade the half plane that includes (0,0). If the inequality is false for (0,0), then shade the half plane that does not include (0,0). If (0,0) is on the line, then follow the same procedure using (1,0) or (0,1) whichever is not on the line.
Example
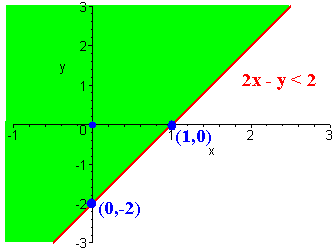
Sketch the solution to
2x - y < 2
Solution
-
We have
x y 0 -2 1 0
-
We plot the points (0,-2) and (1,0) in the xy-plane.
-
Since the inequality is "<", we connect the points with a solid line.
-
(0,0) is not on the line. We test:
2(0) - (0) < 6 or 0 < 6
Since this statement is true, we can shade in the half plane containing (0,0). This is the half plane above the solid line.
Example
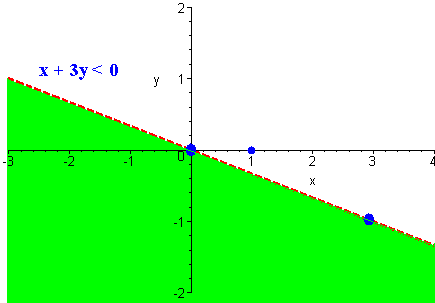
Sketch the solution to
x + 3y < 0
Solution
-
Since (0,0) is on the graph, we pick a second point, letting x = 3 so that we can avoid fractions.
x y 0 0 3 -1
-
We plot the points (0,0) and (3,-1) in the xy-plane.
-
Since the inequality is "<", we connect the points with a dotted line.
-
(0,0) is on the line. We test instead the point (1,0).
1 + 3(0) < 0 or 1 < 0
Since this statement is false, we can shade in the half plane not containing (1,0). This is the half plane below the solid line.
Exercises
Sketch the solution of the following
2x + y > 10
x + y < 2
x + 4 > 2
y - 6 < 1
e-mail Questions and Suggestions