Coordinates and Graphs of Lines
Solutions to Equations in Two Variables
Example
Consider the equation
2x + y = 10
We see that when
x = 3 and
y = 4
we have
2(3) + 4 = 10
is true. We say that (3,4) is a solution to the equation.
We call (3,4) and ordered pair. The first number represents the
x value
and the second number represents the y value. Notice that the ordered
pair (1,2) does not satisfy the equation since
2(1) + 2 = 4
which is not 10.
Exercise
Which ordered pairs satisfy the equation
4x + 3y = 24
-
(3,5)
-
(6,0)
-
(3,4)
![]()
T Tables
To find ordered pairs that satisfy the equation, we first solve (if possible)
for y in terms of x. Then we construct a T Table that consists of two
columns. The first represents the x coordinate and the second column
represents the y coordinate.
Example
Given that
2x - y = 4
we solve for y:
-y =
-2x + 4
Subtract 2x from both sides
y =
2x - 4
Multiply by
-1
Now we construct a table by plugging in several values of x and find y:
x = 0: y = 2(0) - 4 = -4
x = 1: y = 2(1) - 4 = -2
x = 2: y = 2(2) - 4 = 0
x = 3: y = 2(3) - 4 = 2
x = -1: y = 2(-1) - 4 = -6
We create our table:
| x | y |
| 0 | - 4 |
| 1 | - 2 |
| 2 | 0 |
| 3 | 2 |
| -1 | - 6 |
This is called a T-table.
Exercise
Construct a T-Table for
2y - 6x = 8
The Coordinate Axes and Graphing
Just as we draw a number line to represent real numbers, we can also represent ordered pairs. We draw two number lines that intersect each other at right angles. We call the plane that the two number lines lie in the xy-plane. We call the horizontal line the x-axis and the vertical line the y-axis. We let the right of the x-axis represent positive x values, while the top of the y-axis represents positive y values. The intersection point is where x = 0 and y = 0 is called the origin. The top right part of the plane is called Quadrant I. The top left part of the plane is called Quadrant II. The bottom left part of the plane is called Quadrant III. The bottom right part of the plane is called Quadrant IV. To represent an ordered pair (x,y) on the xy-plane, we walk x units to the right and y units upward. Below are the points (1,2), (-1,1), (-2,-1), and (2,-1) plotted on the xy-plane.
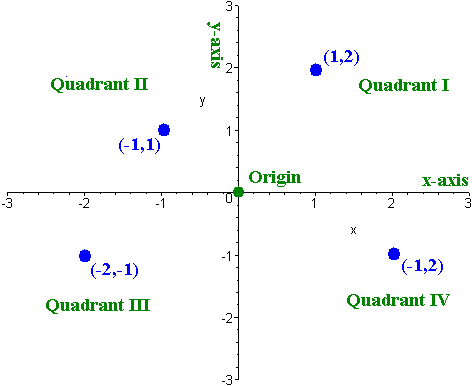
|
Definition The graph of an equation the collection of points (a,b) on the xy-plane such that (a,b) is a solution to the equation. |
Theorem An equation of the form |
Remark: We usually plot the point where x = 0
(called the
y-intercept) and the point
where y = 0 (called the x-intercept.)
Example:
Graph
2x - 3y = 6
Solution:
We have the T-Table with the two points.
| x | y |
| 0 | -2 |
| 3 | 0 |
We see that the x-intercept is at (3,0) and the
y-intercept is at (0,-2).
Next we plot these points on the xy-plane and connect the dots.
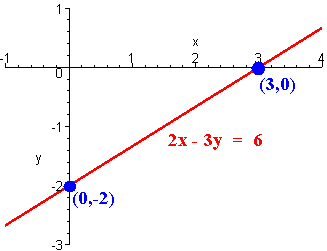
Horizontal and Vertical Lines
Horizontal and vertical lines have special equation that we describe below.
Definition
An equation of the form
An equation of the form |

Back to the Math Department Home
e-mail Questions and Suggestions