The Number Line, Absolute Value, Inequalities, and Properties of R
The Number Line
To draw a number line we draw a line with several dashes in it and ordered
numbers below the line, both positive and negative. The number
corresponding to the point on the number line is called the coordinate
of the number line.

Absolute value signs make the inside positive:
|-3| =
3 |2| = 2
|4 - 1| = |3| = 3
We can write
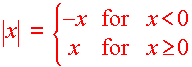
|
We can read this as "Multiply by (-1) if x
is
negative, and leave it alone if x is positive."
Recall the four inequalities:
| Symbol | Meaning |
| < | Less Than |
| > | Greater Than |
| < | Less Than or Equal to |
| > | Greater Than or Equal to |
When we graph an inequality on a number line we use "[" or
"]" to include
the point and "(" or ")" to not include the point.
For example, [1, 3) means all, the points
between 1 and 3
including 1 but not including 3. We
can write this on the number line as

The link below
will help you investigate the number line and interval notation:
The
Number Line and Inequalities
Exercises
Graph the following on a number line
-
{x| x < 3}
-
{x| x > 2}
-
{x| 3 < x < -5}
-
{x| |x| > 4}
Properties of Addition and Multiplication
-
-
Addition: a + b = b + a
-
Multiplication: ab = ba
-
-
-
Addition: (a + b) + c = a + (b + c)
-
Multiplication: (ab)c = a(bc)
-
-
-
Addition: there is a 0 such that a + 0 = 0 + a = a
-
Multiplication: there is a 1 such that a1 = 1a = a
-
-
-
Addition: for any a, there is a -a with a + -a = 0
-
Multiplication: for any a not 0, there is a 1/a with a(1/a) = 1
-
-
-
a(b + c) = ab + ac
-
(a + b)c = ac + bc
-
-
Trichotomy
If a and b are real numbers then one of the three must hold-
a < b
-
a > b
-
a = b
-
-
Transitivity
If a, b, and c are real numbers and
a < b and b < c
then
a < c
Examples
(2 + 3) + 4
= 2 + (3 + 4)
(Associative Property of Addition)
(x - y)(x + y)
= (x + y)(x - y) (Commutative Property of Multiplication)
1
(2 - y)
= 1 (Multiplicative inverse)
2 - y
Exercises:
Complete the following. (If you hold your mouse on the yellow rectangle,
you will see the solution.)
-
x - z = ________ (Commutative)

-
w (0) = _________ (Multiplication property of 0)

-
3 (xy) = __________ (Associative)

-
x (y - 3) = _________(Distributive)

e-mail Questions and Suggestions