Sets

Set Definitions


The idea of a set is on of the fundamental concepts of mathematics.  Below, we stat the difinition.

Definition  

A set is a well defined collection of objects.   

 

Notation:  

        A = {2,7,1}         B = {cat, dog, mouse}        C = {2,4,6,8,10,...100}

        D = {1,3,5,7,9,...}         E = {}

The set E is called the empty set.

We say that 

       

to mean that "6 is an element of C"
and

        

 means "Horse is not an element of B."

 

Types of Numbers

  • We define the natural numbers to be

            N      =  {1, 2, 3, 4, 5, 6, ...}

  • We define the whole numbers to be

            W  =  {0, 1, 2, 3, 4, 5, ...}

  • We define the set of integers as

            Z  =  {... -2, -1, 0, 1, 2, 3, ...}
    So that the integers consist of the whole numbers and their negatives.

  • We define the set of rational numbers  as the collection of all fractions.  Formally we have

            Q = { p/q | p in Z , q in Z - {0}}

Examples of Rational Numbers  

        3/4, 2/5, -3/2, 7, 0

Are there other numbers?  What numbered squared equals?

       

is not a rational number.  


We define the set of real numbers by

     R = {All numbers that can be put on the number line so that the 
               number line has no holes}

We define the irrational numbers as the real numbers that are not rational


Set Notation

      

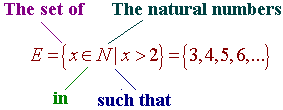
We read, "The set of all x in the natural numbers such that x is greater than 2"

Subsets

A is a subset of B, A C B if every element of A is also an element of B.

Exercise

  
Let 
        A = {1,2,3), B = {0,1,2,3,4} and C = {2,3,4}

Which of the following is true?  (let your mouse rest on the yellow box for a few seconds to see the solution.)

  1. A C B        True, since 1,2, and 3 are also in B.

  2. B C A        False, since 0 and 4 are not in A.

  3. C C B        True, since 2, 3, and 4 are also in B.

  4. A C C        False, since 1 is not in C.

Note that we have the following chain:

N C W C Z C Q C R


Unions

We define A U B  "A union B" to be the set of all elements either in A or B.

Example  
 Let 

        A = {1, 2, 3}          B = {2, 3, 4}

then 

        A U B  =  {1, 2, 3, 4}

Intersections

We define A I B, "A intersection B" to be the set of all elements that are in both A and B.
        A I B  =  {2, 3}  

from the previous example.  We can write

        A U B  =  {x | x in A or x in B}

        A I B  =  {x | x in A and x in B}

 

Next we will discuss Venn Diagrams

To further explore with set definitions go to http://mathcsjava.emporia.edu/~godbocat/setOperations.html

 

Back to Math 152A Home Page

e-mail Questions and Suggestions