Linear Inequalities, Variation, and Solving by Graphing
Definition of a Linear Inequality
|
Definition A linear inequality is an inequality that has one of the four forms below
|
We follow the follow the procedure listed below to graph the inequality:
Solving Linear Inequalities
Steps for solving Inequalities
-
Write a T-table plotting the x and y intercepts (find where x = 0 and where y = 0). If the equation gives (0,0) as a point, plot another convenient point such as when x = 1.
-
Plot the two points on the xy-plane.
-
If the inequality is "<" or ">" then connect the two points with a dotted line. The dotted line is analogous to the open circle on the number line. Otherwise, connect the two points with a solid line. The solid line is analogous to the closed disk on the number line.
-
If (0,0) is not on the line, substitute (0,0) into the inequality to see if it is true for (0,0). If it is true, shade the half plane that includes (0,0). If the inequality is false for (0,0), then shade the half plane that does not include (0,0). If (0,0) is on the line, then follow the same procedure using (1,0) or (0,1) whichever is not on the line.
Example
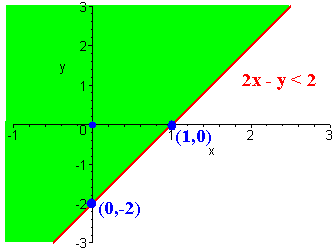
Sketch the solution to
2x - y < 2
Solution
-
We have
x y 0 -2 1 0
-
We plot the points (0,-2) and (1,0) in the xy-plane.
-
Since the inequality is "<", we connect the points with a solid line.
-
(0,0) is not on the line. We test:
2(0) - (0) < 6 or 0 < 6
Since this statement is true, we can shade in the half plane containing (0,0). This is the half plane above the solid line.
Example
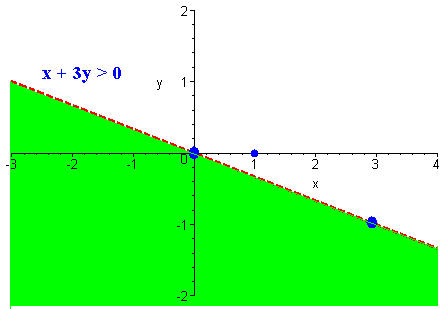
Sketch the solution to
x + 3y > 0
Solution
-
Since (0,0) is on the graph, we pick a second point, letting x = 3 so that we can avoid fractions.
x y 0 0 3 -1
-
We plot the points (0,0) and (2,-1) in the xy-plane.
-
Since the inequality is ">", we connect the points with a solid line.
-
(0,0) is on the line. We test instead the point (1,0).
1 - 3(0) < 0 or 1 < 0
Since this statement is false, we can shade in the half plane not containing (1,0). This is the half plane below the solid line.
Exercises
Sketch the solution of the following
2x + y > 10
x + y < 2
x + 4 > 2
y - 6 < 1
Now try to put the following inequalities on the same plane.
-
3x - y < 9 and 4x+ y > 4
-
2x - y > 10 and x + y < 3
Some Terminology
In word problems there are a few phrases that come up often enough to give them special focus. Here is the dictionary:
| Phrase | Math |
| varies directly as | = k times ___ |
| is proportional to | = k times ___ |
| varies inversely as | = ___/k |
| is inversely proportional to | = ___/k |
| varies jointly as A and B | = kAB |
We call k the constant of proportionality. k reflects the unit system we are working with.
Remember the first step after reading the word problem is to label the variables.
Examples
-
The intensity of sound varies inversely as the square of the distance from the source.
We let
r = the distance from the source
I = the sound intensity
then
k
I =
r2
-
The voltage of a circuit is directly proportional to the current.
Let
V = the voltage
I = the current
then
V = kI
-
The area of a circle varies directly as the square of the radius.
We let
A = area of the circle
r = the radius
Then
A = kr2
You probably know what famous constant k is.
-
The time that it takes to arrive is inversely proportional to the speed at which we travel
We let
t = the time it takes to arrive
s = speed we are traveling
then
k
t =
s -
The Volume of a right circular cylinder varies jointly as the square of the radius and the height.
We let
V = the volume of the cylinder
r = the radius
h = the height
Then
V = kr2 h
Initial Value Problems
Sometimes, we are given information about the initial conditions of the problem or some other information. We can use this information to find k. After we find k, we can answer the question.
Example
The population of the world varies directly as the time elapsed since 1988. In 2002 the population was 7 billion. What will it be in the year 2018?
Solution
Let P be the population of the world and t be the years since 1988.
The
P = kt
Using our initial value conditions (note that 2002 is 14 years after 1988),
7 = k(14)
k = 1/2
In 2018, t = 30 hence
P = 1/2(30) = 15 billion.
There will be 15 billion people in the year 2018.
Exercises
-
The volume of an expanding balloon is directly proportional to the time since a person begins blowing it up. If after 1 second the volume of the balloon is 10 cu inches. How large will it be after 3 seconds?

-
The amount of water flowing down a waterfall varies jointly as the speed at which the water is flowing and the cross sectional surface area of the flow. Suppose that at the top of the falls where the water is traveling at a rate of 2 feet per second and has a cross sectional surface area of 10 square feet, there is 100 cu feet per second flowing out of the falls. How many cubic feet per second is the water flowing at the bottom of the falls where the water is traveling at a rate of 50 feet per second but has a surface area of only 0.4 square feet?

Solving by Graphing
If we want to solve a system of equations, we can graph them and find the point of intersection.
Example
Solve
x - 2y = 3
2x - y = 7
We just graph the two equations and eyeball the intersection point.
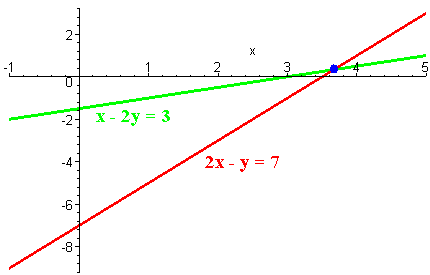
The point of intersection looks like it has coordinates approximately (3.7,0.5). This is only an estimate. The next section will show us how to find the exact solution
Back to the Quadratic Functions and Linear Inequalities Page
Back to the Basic Algebra Part II Page