Formulas and Absolute Value Inequalities

 

Problem Solving With Formulas

A formula is an equation that relates real world quantities.  

Examples

        P  =  2l + 2w 

is the formula for the perimeter P of a rectangle given the length  l and width w.

        d  =  rt 

is the formula for the distance traveled d given the speed s and the time t.

        A  =  P + Prt 

is the formula for the amount A in a bank account t years after P dollars is put in at an interest rate of r.

        V  =  pr2h 

is the formula for the volume V of a cylinder of radius r and height h, where p @ 3.14.

                   h
        A  =         (b1 + b2) 
                   2

is the formula for the area A of a trapazoid with height h and bases b1 and b2.

 

We say that a formula is solved for a variable x if the equation becomes 

        x   =  stuff 

where the left hand side does not include any x's.  


Example

Solve 

        C = 2pr 

for r then determine the radius of a circle with circumference 4.

Solution

Divide both sides by 2p:

             C
                      =  r
            2p

Use the reflexive property to get

                   C
        r  =                  
                  2p

Now plug in 4 for C to obtain

                    4              2
        r  =               =           
                  2p             p 

 


Steps for Solving a Word Problem

  1. Read the problem, sketch the proper picture, and label variables.

  2. Write down what the answer should look like.

  3. Come up with the appropriate formula.

  4. Solve for the needed variable.

  5. Plug in the known numbers.

  6. Answer the question.


Example:  

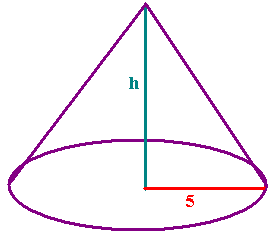
A pile of sand has the shape of a right circular cone.  Find the height of the pile if it contains 100 cc of sand and the radius is 5 cm.

Solution:


  2. The height of the pile is ________ cm.

  3. We use the formula for the volume of a right circular cone:  

            V  =  1/3 pr2h.

  4. Multiply by 3 on both sides to get  

            3V  =  pr2h.

    Divide both sides by pr2 to obtain

                3V                                   3V
                         =  h         or      h  =                 
                pr2                                   pr2  

  5.             3(100)              12
    h =                       =                    
                   p52                 p       

  6. The height of the pile is 12/p cm. 


Absolute Value Inequalities

Step by Step:

Step 1:  Solve as an equality.

Step 2:  Plot the points above the number line.

Step 3:  If the relation is < then include the middle portion.  If the relation is > include the outside ends.  

Step 4:  Graph on the number line remembering to put an open or closed dot when necessary.

 

Example:

  1. Graph the inequality

      |x| < 4

    We proceed as follows:

    1. We have     x = 4     or     x = -4.

    2.  Since the relation is "<" we include the middle portion and put open circles.



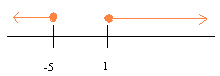
  2. Graph the inequality

      |2x + 4|  >  6

    1. We have     

      2x + 4  =  6     or     2x + 4  =  -6

    2. 2x  =  2         or         2x  =  -10

      so

      x  =  1       or       x  =  -5

      We graph the solution on a number line including the outer regions and putting a closed dot at the endpoints.  

       

       

Exercises

Graph the solution set of the following.

  1. |2x + 1|  >  3    x < -2 or x > 1



  2. |3x - 2|  >  4     x < -2/3 or x > 2



  3. |2x - 1|  >  -2    All Real Numbers



  4. | 5x + 4|  <  -3   No Solution

 

Back to the Factoring and Rational Expressions Page

Back to the Basic Algebra Part II Page

Back to the Math Department Home Page

e-mail Questions and Suggestions