Equations of Lines
Parallel and Perpendicular Lines
|
Definition:
|
Remark: If m1 is the slope of the first line and m2 is the slope of the second line, then
1
m1 =
-
m2
We can also say that two lines are perpendicular if
m1m2 = -1
This definition does not apply to vertical and horizontal lines. Any two distinct vertical lines are parallel and any two distinct horizontal lines are also parallel. Any vertical line is perpendicular to any horizontal line.
Example
Determine which of the lines that pass through the given
points are parallel, and which are perpendicular.
Line 1: P = (2,3) Q = (1,5)
Line 2: P = (4,6) Q = (2,5)
Line 3: P = (-3,2)
Q = (1,4)
Solution
We compute the slopes of the three lines
5 - 3
m1 =
= -2
1 - 2
5 -
6
1
m2 = =
2 -
4
2
4 -
2
1
m3 =
=
1 - (-3) 2
Since
m2 = m3
Line 2 and Line 3 are parallel.
Since
m1m3 = -1
Line 1 and Line 3 are perpendicular. Also Line 1 and Line 2 are perpendicular.
Equations of Lines
If we are given two points, how can we find the equation of the line passing through the two points? If we know the slope and a point (x1, y1) we have that
rise
y - y1
m =
=
run
x - x1
Now multiplying by
x - x1
on both sides of the equation results in the following formula.
|
Point Slope Formula for the Equation of a Line y - y1 = m (x - x1) |
Example
Find the equation of line through the point (1,2) with slope 4.
Solution:
We use the formula:
y - 2 = 4(x - 1) = 4x - 4
Hence
y = 4x - 4 + 2 = 4x - 2.
Step by Step Procedure:
Step 1: Use the slope formula to find the slope m.
Step 2: Plug the first point and the slope into the point slope formula.
Step 3: Simplify to get into the form y = mx + b.
Example:
Find the equation of the line passing through the points
(1,4) and (2,9).
-
We find
9 - 4
m =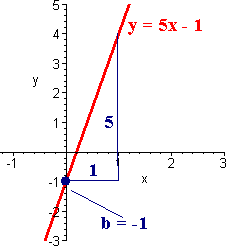
2 - 1
-
We plug into the formula:
y - 4 = 5(x - 1)
-
We have
y - 4 = 5x - 5
y = 5x - 1
We see that if the equation is in the form
y = mx + b
then m is the slope and b is the y intercept.
In the above example, the slope is 5 and the y intercept is -1.
Exercises
-
Find the equation of the line through the point (1,2) that is perpendicular to the line
y = 3x - 4

-
Find the equation of the line through the point (3,4) that is parallel to the line
3x - 2y = 5

Application:
At your hotel if you charge $100 per night you can fill 80 of your rooms while if you charge $90 per night you can fill 85 of your rooms. Assume that the vacancy and the price are linearly related.
-
Come up with an equation that predicts how many rooms y you will fill for a given price x.
-
How many rooms will you fill if you charge $120 per night.
Solution:
-
We have the two points (100,80) and (90, 85).
We compute the slope:
85 - 80 5 1
m =
90 - 100 -10 2Then we use the point slope formula:
y - 80 = -1/2 (x - 100)
y - 80 = -1/2 x +50
y = -1/2 x + 130
-
We plug in 120:
y = -1/2 (120) + 130 = 70
Therefore, at $120 we can expect to fill 70 of our rooms.
e-mail Questions and Suggestions