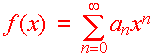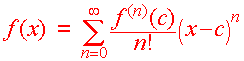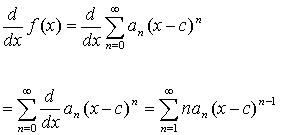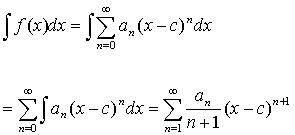Power Series
Definition of a Power Series
We now investigate a generalization of polynomials. The polynomial
below is a fifth degree polynomial
3x5 - 2x4 + 5x3 + 4x - 1
if instead of a fifth degree polynomial, we consider a polynomial of infinite degree.
Definition of a Power Series |
More generally, if f(x) is represented by the series
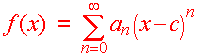
Then we call f(x) a power series centered at x =
c.
Examples
The power series
![]()
is centered at 0.
The power series
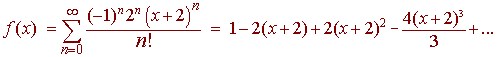
is centered at -2.
The Radius of Convergence
Next we want to investigate the domain of power series. Recall to find
the domain, we ask what values of x can the
function handle? This is particularly important with power series, since
infinite series often do not converge. It would be an insurmountable task
to plug in each value of x and see if the series
converges for that value. Fortunately, we have the following theorem.
Theorem
If
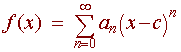
is a power series centered at c then only the following three are possibilities for the domain of f.
-
The domain is the value c only.
-
There domain is all real numbers.
-
There exists a real number R such that all values of x that satisfy
| x - c | < R
are in the domain and values that satisfy
| x - c | > R
are not in the domain.
R
is called the radius of convergence of f.
To compute the radius of convergence, we use the ratio test.
Example: Find the radius of convergence of
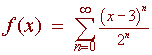
Solution
We use the Ratio Test:
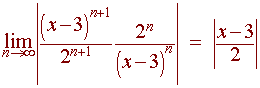
We solve
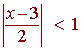
or
|x - 3| < 2
so that
1 < x < 5
Since
1/2(5 - 1) = 2
the radius of convergence is 2
Exercise:
Find the radius of convergence of
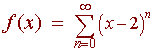
Taylor and Maclaurin Series
Since power series are functions, a natural question to ask is, "Can our everyday functions be represented as power series?" Also, "Given a power series, can we find an everyday function that is equivalent to the power series?"
The following definition helps to answer these questions.
|
Definition The Taylor Series for f(x) centered at x = c is
If c
= 0, then the series is called
the Maclaurin series for f.
|
We use the notation f
(n) to denote
the nth derivative of f.
Example:
Find the McLaurin Series for
f(x) =
cos(x)
Solution
We compute:
f(0) = 1
f '(0) = 0 f ''(0) = -1 f (3)(0) = 0
f (4)(0)
= 1 f (5)(0) = 0 f (6)(0) =
-1 f (7)(0) = 0
f (8)(0)
= 1 f (9)(0) = 0
f (10)(0) =
-1 f (11)(0) = 0
Hence we have the series
1 - x2 /2+ x4/4! - x6/6! +
x8/8! - x8/8! + ...
We see that the series is
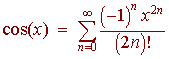
Exercises Find the Taylor series expansion for
-
sin(x) centered at x = 0
-
ln(x) centered at x = 0
Differentiation and Integration of Power Series
Since a power series is a function, it is natural to ask if the function is
continuous, differentiable or integrable. The following theorem
answers this question.
|
Theorem:
and |
Example:
Consider the series
f(x) = Sxn
by the GST this series converges for |x| <
1, hence the center of convergence is 0 and the radius is
1.
By the above theorem
f '(x) = Snxn-1
has center of convergence 0 and radius of convergence
1 also. We can also say that
![]()
also has center of convergence 0 and radius of convergence
1.
Exercise:
Show that
![]()
satisfies the differential equation
y'' + xy' - y = 0
We can also use substitution to find power series.
Example
Find the Maclaurin series for
1
1 - x2
Solution
Substituting x2 for x in
![]()
we have
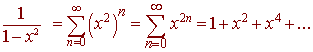
Back to the Math 117 Home Page
Back to the Math Department Home
e-mail Questions and Suggestions