Functions of Two Variables

I.  Homework

II.  Planes

Recall that a line is given by the first degree polynomial ax +by = c

similarly, a plane is given by the first degree polynomial ax + by + cz = d

to graph a plane, plot the x, y, and z intercepts.  

Example:  Sketch the graph of the plane 2x + 3y + z = 6

We find the x intercept by setting y and z =0,  2x = 6 or x = 3 the x-intercept is

(3,0,0)

Similarly, the y intercept is (0,2,0) and the z intercept is (0,0,6).  Now plot the three points and connect the three points to sketch a triangle that sits in the plane.

IV.  Quadric Surfaces

Recall that the quadrics or conics are lines , hyperbolas, parabolas, circles, and ellipses.  In three dimensions, we can combine any two of these and make a quadric surface.  For example

z = x² + y²

is a paraboloid since for constant z we get a circle and for constant x or y we get a parabola.  We use the suffix -oid to mean ellipse or circle.  We have:

x²/a² + y²/b² + z²/c² = 1 is an ellipsiod       

-x²/a²  - y²/b² + z²/c² = 1 is a hyperboloid of 2 sheets while

x²/a² + y²/b² - z²/c² = 1 is a hyperboloid of 1 sheet

III.  Definition of Functions of Several Variables

A function of several variables is a function where the domain is a subset of Rⁿ and range is R.

Example:  

f(x,y) = x - y is a function of two variables

g(x,y,z) = (x - y)/(y - z)

is a function of three variables.

IV.  Finding the Domain

To find the domain of a function of several variables, we look for zero denominators and negatives under square roots:

Example

Find the domain of f(x,y) = sqrt(x - y)/(x + y)

The first we have x - y > 0

second we have x + y not= 0 hence we need to stay off the line y = -x

The domain is {(x,y)| x - y > 0 and y not= -x}

Exercise

Find the domain of the function f(x,y,z) = xyz/sqrt(4 - x² - y² - z²)

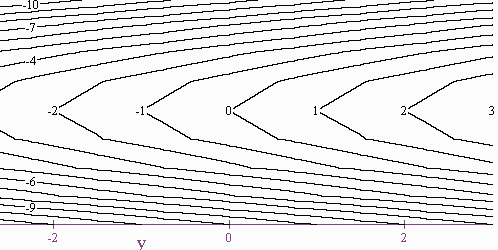
V.  Level Curves

A map will be shown of the desolation wilderness that represents the function that maps a longitude and latitude to an altitude.  We will investigate what the contour lines mean.  

We will make our own contour map of the function

f(x,y) =  y - x² by setting constant values for z:

When z = 1, we have y = x² + 1

When z = 2, we have y = x² + 2