Math 117 Practice Midterm 2
Please work out each of the given problems. Credit will be based on the steps that you show towards the final answer. Show your work.
Problem 1
The following table gives the probability distribution for the number of kittens in a litter.
| Number x in Litter | 1 | 2 | 3 | 4 | 5 | 6 |
| P(x) | 0.05 | 0.12 | 0.24 | 0.35 | 0.20 | 0.04 |
Determine E(x) and s. Explain the meaning of each.
We expand the table as follows
| Number x in Litter | 1 | 2 | 3 | 4 | 5 | 6 | Totals |
| P(x) | 0.05 | 0.12 | 0.24 | 0.35 | 0.20 | 0.04 | |
| xP(x) | 0.05 | 0.24 | 0.72 | 1.40 | 1.00 | 0.24 | 3.65 |
| (x - 3.65)2 | 7.02 | 2.72 | 0.42 | 0.12 | 1.82 | 5.52 | |
| (x - 3.65)2(P(x)) | 0.35 | 0.33 | 0.10 | 0.04 | 0.36 | .22 | 1.40 |
The expected value is 3.65. This means that the overall average number of kittens in a litter is 3.65 kittens.
The variance is 1.40. We take the square root to get the standard deviation of 1.18.
Problem 2
You have experimented with the days for germination for a lupin and know that the distribution follows the parabolic distribution
f(t) = kt(1 - t) for 0 < t < 1
where t is measured in months and k is a positive constant.
A. Find k.
To find k we set the integral equal to zero.
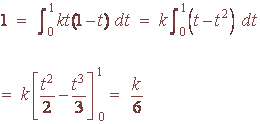
Hence k = 6.
B. Find the probability that a lupine seed will germinate between 0.3 and 0.5 months.
We find
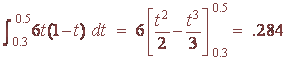
Hence
P(0.3 < x < 0.5) = 0.284
C. Find the expected value E(t) and interpret what it means.
We find
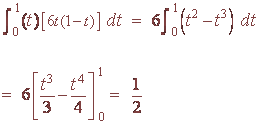
Hence
E(t) = 0.5
D. Find the standard deviation.
We calculate the integral
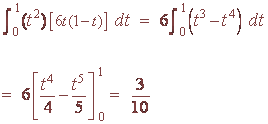
Now calculate the variance
V = 0.3 - 0.25 = 0.05
Take a square root to get the standard deviation of 0.22.
Problem 3
Currently, the benefit package costs the college $9442 and is expected to increase 20% next year. Assume the 20% increase becomes a trend over the next several years.
A. Write an expression for the cost of the benefit package after n years.
Notice that a 20% increase means that the next year will have 1.2 times the current year, since you have 100% of your expense from last year plus an additional 20%. Look at the first few terms.
a0 = 9442 a1 = (9442)(1.2)
a2 = (9442)(1.2)2 a3 = (9442)(1.2)3
Hopefully the pattern is apparent. The general term is
an = (9442)(1.2)n
B. Compute the cost of benefits in the year 2020. (This year is 2004).
The year 2020 corresponds with n = 2020 - 2004 = 16.
a16 = (9442)(1.2)16 = 174568
We can expect that the benefit package will cost $174,568 if trends continue.
Problem 4
Determine the convergence or divergence of the following series.
A. 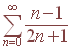
We take the limit using L'Hopital's rule:
![]()
Since the limit is not zero, the series diverges.
B. ![]()
This is a geometric series with r = 1/3, hence by the geometric series test the series converges.
C. 
![]()
S
Problem 5
Explain why the series converges. Then approximate the following sum using 5 terms. Then estimate the maximum error of your approximation.

This is a p-series with p = 8 > 1, hence by the p-series test the series converges.
We find
![]()
We compute the maximum error by finding
