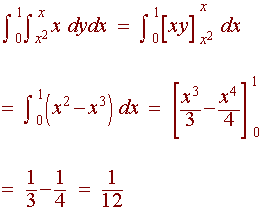Math 117 Practice Midterm I

Please work out each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Show your work.

Problem 1

Let

        f(x,y)  =  xy - ln(2x - y)

Find

A. 

Solution

We treat y as the variable and x as a constant.  We get

                                     -1
        f_y(x,y)  =  x -                   
                                  2x - y

Now plug in (3,-1) to get

                                     -1                     20
        f_y(x,y)  =  3 -                         =            
                                 2(3) - (-1)              7

B.   

Solution

We first find the partial derivative with respect to x.

                                     2
        f_x(x,y)  =  y -                    =  y - 2(2x - y)^-1
                                  2x - y

      Now find the derivative of the above with respect to x.

        f_xx  =  0 - 2(-1)(2x - y)^-2(2)  =  4(2x - y)^-2

C.    f_xy(x,y)

Solution

We take the derivative with respect to y of f_x (computed in the first half of part B).

        f_xy  =  1 - 2(-1)(2x - y)^-2(-1)  =  1- 2(2x - y)^-3

Problem 2

Find the length of the sides of the triangle with vertices (1,-1,2), (3,1,5), and (-1,2,4) and determine whether the triangle is a right triangle, isosceles triangle, or neither of these.

Solution

We use the distance formula to calculate the squares of the three lengths:

        (1,-1,2) to (3,1,5):  (3 - 1)² + (1 - (-1))² + (5 - 2)²  =  4 + 4 + 9  =  17

        (1,-1,2) to (-1,2,4):  (-1 - 1)² + (2 - (-1))² + (4 - 2)²  =  4 + 9 + 4  =  17

        (3,1,5) to (-1,2,4):  (-1 - 3)² + (2 - 1)² + (4 - 5)²  =  16 + 1 + 1  =  18

The square roots are the distances: 

and 17 + 17 does not equal 18.

Problem 3

Name the following surfaces and draw a rough sketch of each.

A.   x² + 4y2  =  36 + 9z²

Solution

We bring the terms to the left hand side and divide by 36 to get

            x²           y²           z²
                   +             -                 =  1
            36           9            4

This is a hyperboloid of one sheet.  The sketch is shown below.

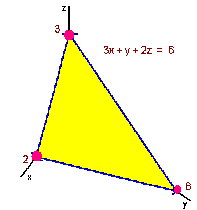
B.  3x + y + 2z  =  6

Solution

This is a plane with intercepts (2,0,0), (0,6,0), and (0,0,3).  We graph it by plotting the intercepts and connecting the dots.

Problem 4

Use a graphing calculator to draw at least five level curves for the following function.  Copy them on the test and describe in words to what extent the surface rises above or below the paper.  Describe in words how the surface differs from quadrant to quadrant.

                          1
        f(x,y)  =             
                         xy²

Solution

Below is a contour map of f(x,y)

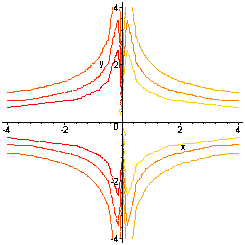
The surface is above the xy-plane in the first and third quadrants and below the xy-plane in the second and fourth quadrant.  The axes act as asymptotes, for example as a point moves towards the y-axis from the first quadrant, the surface rises to infinity.  As the point moves towards the y-axis from the second quadrant, the surface falls to negative infinity.

Problem 5

Locate and classify the critical points of

        f(x,y)  =  x² + 2xy + 3y² - 4x - 6y + 5

Solution

We first find

        f_x   =  2x + 2y - 4  =  0

        f_y  =  2x + 6y - 6  =  0

Subtracting the first equation from the second gives

        4y - 2  =  0        y  =  1/2

substituting y  =  1/2 into the first equation and setting it equal to zero gives

        2x + 1 - 4  =  0        x  =  3/2

We have a critical point at (3/2,1/2).

Now we find the second partial derivatives

        f_xx  =  2        f_yy  =  6        f_xy  =  0

We get

        D  =  f_xxf_yy  -  (f_xy)²  =  (2)(6) - 0  > 0

Since f_xx > 0, the point (3/2,1/2) is a local minimum.

Problem 6

Common blood types are determined genetically by three alleles A, B, and O.  A person whose blood type is AA, AB, or AO is homozygous.  A person whose blood type is AB, AO, or BO is heterozygous.  A Hardy Weinberg law states that the proportion P of heterozygous individuals in any population is

        P(p,q,r)  =  2pq + 2pr + 2qr

where p, q, and r represent the proportion of A, B, and C respectively in the population.  Use Lagrange multipliers and the fact that

        p + q + r  =  1

to show that the maximum proportion of heterozygous individuals in any population is 2/3.

Solution

We consider the function

        F(p,q,r)  =  2pq + 2pr + 2qr - l(p + q + r)

and find the critical values of F.  We take partial derivatives

         F_p  =  2q + 2r - l  =  0

        F_q  =  2p + 2r - l  =  0

        F_r  =  2p + 2q - l  =  0

        p + q + r  =  1

Solving for l, and setting the equations equal gives

        2q + 2r  =  2p + 2r  =  2p + 2q

Dividing by 2 gives

        q + r  =  p + r  =  p + q

The equation p + q + r  = 1 gives

        p  =  1 - q - r

Substituting gives

        q + r  =  1 - q - r + r  =  1 - q - r + q

or

        q + r  =  1 - q  =  1 - r

The first equality says that

        r  =  1 - 2q

Substituting into the second equality gives

        1 - q  =  1 - (1 - 2q)  =  2q

so that

        3q  =  1            q  =  1/3

hence

        r  =  1 - 2(1/3)  =  1/3

Since they all add to 1 we get

        p  =  1/3

We plug (1/3,1/3,1/3) back into the original equation to get

        P(p,q,r)  =  2(1/3)(1/3) + 2(1/3)(1/3) + 2(1/3)(1/3)  =  6/9  =  2/3

Problem 7

The number of students taking math at LTCC over the past years is shown in the following table.

A.  Use a calculator to find the least squares regression line for this data.

Solution

The calculator gives

        y  =  9.8x + 110.6

B.  Estimate the number of students that took math in 2003.

Solution

We just plug in 3 for x to get

        y  =  9.8(3) + 110.6  =  140

We predict that in 2003 there were approximately 140 students taking math.

Problem 8

Evaluate the following double integral.  (Hint:  You may need to change the order).

We can not perform this integral in this order, so we need to change the order of integration.  The region is bounded by

        y  =  3x        y  =  9       and      x  =  0

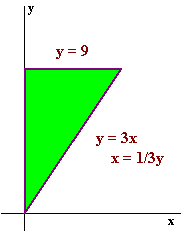
We can integrate to get

We can now use substitution with

        u  =  y²     du  =  2ydx

to get

Problem 9

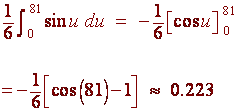
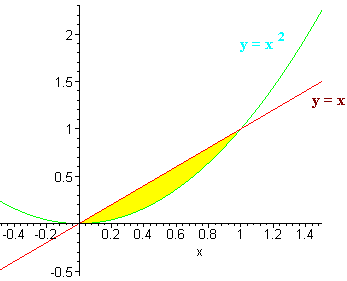
Use a double integral to find the volume of the solid bounded by

        z  =  x,    z  =  0,    y  =  x,     and    y  =  x²  

Solution

We first graph the region (shown below).  Notice that the region is in the xy-plane, while the function that we will integrate over is 

        z(x,y)  =  x

Notice that the top curve is 

        y  =  x

and the bottom is 

        y  =  x² 

And x ranges from 0 to 1.  Hence the integral is