Practice Final
Please work out each of the problems below. Credit will be based on the steps towards the final answer. Show your work.
Problem 1
Sketch the following.
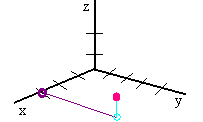
A. The point (3,4,1).
Solution
We draw the xyz-axes, the shadow at the point (3,4) in the xy-plane and move it up 1 unit.
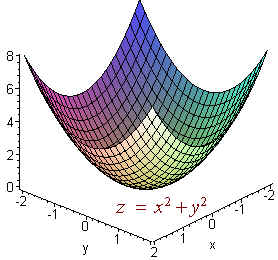
B. The surface z = x2 + y2
Solution
This is a paraboloid with the z-axis as its central axis. The graph is shown below.
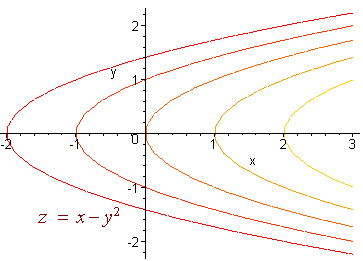
C. Five level curves to the surface z = x - y2
Solution
Draw a table as follows
| k | -2 | -1 | 0 | 1 | 2 |
| k = x - y2 | x = y2 - 2 | x = y2 - 1 | x = y2 | x = y2 +1 | x = y2 + 2 |
Notice that these are all sideways parabolas with distinct x-intercepts that correspond to the value of k. The graphs below show these level curves.
Problem 2
Find fxz for
f(x,y,z) = x2z + y2 - y cos(xz)
Solution
We first find the derivative with respect to x by letting y and z be constant.
fx = 2xz + yz sin(xz) Note the chain rule, the derivative of xz is z
Now find the derivative of this with respect to z,
fxz = 2x + y sin(xz) + xyz cos(xz) We used the product rule for the second term
Problem 3
A swimwear store sells both men's and women's swimsuits and has determined that the profit, P, it can make in stocking x men's suits and y women's suits is
P(x,y) = 2x2 + y2 + xy - 900x - 1100y + 400,000
Determine the number of men's and the number of women's suits that should be stocked in order to maximize profit. Then determine the maximum profit.
Solution
We find the partial derivatives and set them equal to 0.
Px = 4x + y - 900 Py = 2y + x - 1100
This gives us the two equations
4x + y - 900 = 0 x + 2y - 1100 = 0
The first equation can be written as
y = 900 - 4x
Substituting into the second equation gives
x + 2(900 - 4x) - 1100 = 0
x + 1800 - 8x - 1100 = 0
7x = 700
x = 100
Hence
y = 900 - 4(100) = 500
The store should stock 100 men's suits and 500 women's suits.
The profit will be
P(100,500) = 2(100)2 + (500)2 + (100)(500) - 900(100) - 1100(500) + 400,000
= 80,000
Problem 4
A medical researcher is studying the effect that exercise has on a women's percent body fat. The table below shows the results of the corresponding study done. Determine the least squares regression line for this data and use it to estimate the mean percent body fat for a women that exercises 3 hours per week.
| Exercise Hours | 0 | 1 | 2 | 4 | 4 | 5 |
| % Body Fat | 31 | 28 | 26 | 20 | 18 | 15 |
Solution
We use a calculator to find the equation of the regression line.
y = -3.155x +31.414
We plug in x = 3 to get
y(3) = -3.155(3) + 31.414 = 21.95
We predict that the expected percent body fat for a women who exercises three hours per week is 21.95%.
Problem 5
Switch the order of integration to evaluate the following
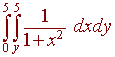
Solution
To change the order we first draw the region shown below.
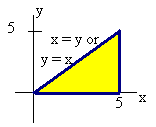
Now we switch the order using dydx. Notice that y goes from 0 to x and x goes from 0 to 5. We have
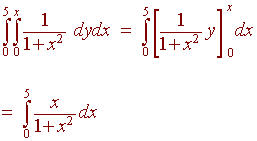
This integral can be solved using substitution with
u = 1 + x2 du = 2xdx
This gives
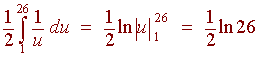
Problem 6
Consider the following game. Pick a card. If you select a face card (Jack, Queen, or King) you win $3. Otherwise, you lose $1. Find the expected value and comment on how this number shows whether playing this game many times is a good idea.
Solution
We write down the probability distribution table
| x | 3 | -1 |
| P(x) | 3/13 | 10/13 |
The expected value is just
3
10
1
3
+ (-1)
= -
13
13
13
Since this is a negative value, we would expect to lose money on the average.
Problem 7
Consider the following probability density function
f(x) = x + 0.5 0 < x < 1
A. Find P(0.5 < x < 1).
Solution
We just find the integral
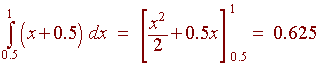
B. Find the standard deviation.
Solution
First find the mean.
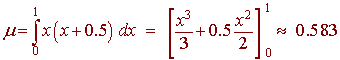
Now calculate the integral using a calculator.
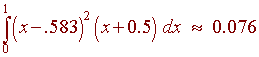
Finally take a square root to get the standard deviation
s = 0.276
C. Find the median.
To find the median we set the following integral equal to 1/2.
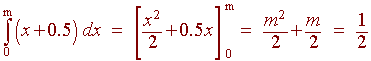
Multiplying by 2 and bringing all the terms to the left hand side gives
m2 + m - 1 = 0
Using the quadratic formula gives
m = 0.618
Problem 8
A pair of baby rabbits is introduced to an island. Assume that rabbits take two months to reproduce when they have 2 pairs of new baby rabbits. Each month thereafter, the adult rabbits produce two additional pairs of rabbits. Assume that the rabbits never die.
A. Write down the number of pairs of rabbits on the island during the first 6 months.
Solution
We have
1, 1, 3, 5, 11, 21
B. Find constants u and v such that
an = u an-1 + v an-2
Where an represents the number of rabbits after the nth month.
Solution
We just notice that to find the current generation, add the newborns to the prior population. The newborns are coming from rabbits that were alive two months previously. Hence
u = 1 and v = 2
Problem 9
A very long river that runs along a vast area of farming communities has 3000 trout in its first mile. Because of pollutants, each mile contains only 80% of the fish that the previous mile had. so that the second mile has 2400 trout and the third has 1820 trout. Considering the river as running an infinite distance, how many trout live in the river?
Solution
We have a geometric sequence
3000, 2400, 1820, ...
with
r = 0.8 and a = 3000
Hence the sum is
3000
S
=
= 15,000
1 - 0.8
There are 15,000 trout in the river.
Problem 10
Determine whether the following series converge or diverge. Be sure to cite the test that you are using.
A.

Solution
We use the nth term test.
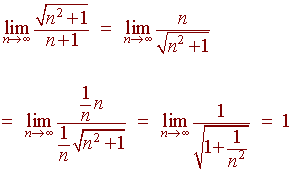
Since the limit does not go to 0, by nth term test, the series diverges.
Solution
We can rewrite this as
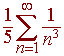
This is a P-series with p = 3 > 1. Hence by the P-Series Test the series converges.
Problem 11
Find a power series representation for
![]()
using the fact that
![]()
then find the radius of convergence for your solution
Solution
We substitute -x2 in for x to get
![]()
Now integrate to get
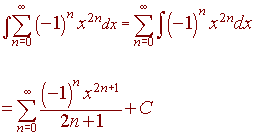
Problem 12
Find the third degree Taylor polynomial centered at x = 0 for
f(x) = x ex
Solution
We find the derivative of f and evaluate them at x = 0.
f '(x) = ex + x ex = ex(1 + x) f '(0) = 1
f ''(x) = ex + (1+ x) ex = ex(2 + x) f '(0) = 2
f '''(x) = ex + (2+ x) ex = ex(3 + x) f '(0) = 3
We now plug this into the Taylor polynomial formula to get
0
1
2
3
P3(x)
= x0
+
x1 +
x2 +
x3
0!
1!
2!
3!
1
= x + x2
+ x3
2
Problem 13
Use Newton's method with initial guess of 1 to estimate
![]()
within three decimal places of accuracy by finding the solution to
x2 - 2 = 0
Solution
With
f(x) = x2 - 2
we have
f '(x) = 2x
so that
xn2 - 2
xn+1 = xn -
2xn
With our initial guess of x0 = 1, the table below gives the rest of the values
| x0 | x1 | x2 | x3 | x4 |
| 1 | 1.5 | 1.4167 | 1.4142 | 1.4142 |
Hence 1.414 approximates the square root of 2 accurate up to three decimal places.
Problem 14
Solve the following differential equation
1
y ' -
y = 2x2 + 1
x
Solution
We first find the integrating factor

now multiply through by the integrating factor to get
1
1
1
y ' -
y = 2x +
x
x2
x
so that
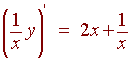
Now integrate both sides to get
1
y = x2 + ln|x| + C
x
and finally multiply both sides by x to get
y = x3 + x ln|x| + Cx
Problem 15
The rate of growth of a bacteria is equal to the quotient of the number of bacteria present and one more than the number of hour that the bacteria has been growing. If initially there were 5 grams of bacteria, how many grams of bacteria will there be in 8 hours?
Solution
We have the differential equation
dx x
=
dt
1 + t
Now separate the variables to get
dx dt
=
x 1 + t
Now integrate to get
ln x = ln(1 + t) + C1
Exponentiate both sides to get
x = eln(1 + t) + C1 = eln(1 + t) ec1 = C(1 + t)
We have that when t = 0, x = 5 so that
5 = C(1 + 0) C = 5
so that
x(8) = 5(1 + 8) = 45
There will be 45 grams of bacteria after 8 hours.