First Order Linear Differential Equations

In this section we will concentrate on first order linear differential equations.  This means that only a first derivative appears in the differential equation and that the equation is linear.  Considering x constant, it can be written in the form

        y'  =  my + b

or setting 

        m  =  -p(x)        and        b  =  g(x)

this gives

        y' + p(x)y  =  g(x)

Before we come up with the general solution we will work out the specific example

                 2
        y' +       y   =   ln x
                 x

The strategy for solving this is to realize that the left hand side looks a little like the product rule for differentiation.  The product rule is 

        (uy)'  =  uy' + u'y

This leads us to multiplying both sides of the equation by u which is called an integrating factor.

                               2
                u y' + u        y  = u ln x
                              x

We now search for a u with 

                     2
        u'  =  u       
                     x

or

        du             2
                =            dx
         u              x

Integrating both sides, produces

        ln u  =  2 ln x  =  ln(x²)

        u  =  x²     exponentiating both sides

Going back to the original differential equation and multiplying both sides by x², we get

       x²y' + 2x y  =  x² ln x

Using the product rule in reverse gives

        (x²y)'  =  x² ln x

Now integrate both sides.  Note that the integral of the derivative is the original.  Integrate by parts to get

                                     u  =  ln x           dv  =  x² dx
                                                             du  =  1/x dx       v  =  1/3 x³

 Hence

                      1                     1
        x²y  =           x³ ln x  -         x³  + C
                      3                     9

                   1                    1             C
        y  =            x ln x  -         x  +                Divide by x²
                   3                    9             x² 

Now we will derive the general solution to first order linear differential equations. 

Consider 

        y' + p(t)y  =  g(t)

We multiply both sides by u to get

        uy' + up(x)y  =  ug(x)

We now search for a u with 

        u'  =  up(x)

or

            du
                      =   p(x) dx
             u

Integrating both sides, produces

           exponentiating both sides

Going back to the original differential equation and multiplying both sides by u, we get

        u y' + u p(x) y  =  u g(x)

        (u y)'  =  u g(x)

Solving for y gives

Exercises

Solve the following differential equations

1. y' + 3/x y  =  1 + x
   
2. y' - y  =  2x        y(0)  =  1
   
3. y' +xy²  =  x
   
4. xy'-3y  =  3x + 2

Application

You are the foundation director of the college and oversee an endowment fund that has a continuous donation flow of $30,000 per year..  The fund earns 4% interest and cannot be use for scholarships for ten years. Determine how much money will be in the fund in ten years if currently there is $100,000 in the fund.

Solution

We see that the rate of increase of the fund is the sum of the interest and the donations.  We can write the differential equation as

        A'  =  0.04A + 30,000

where A is the amount of money in the account at time t.  Subtracting, write

        A' - 0.04A  =  30,000

This is a linear first order differential equation.  The integrating factor is

So that the solution is

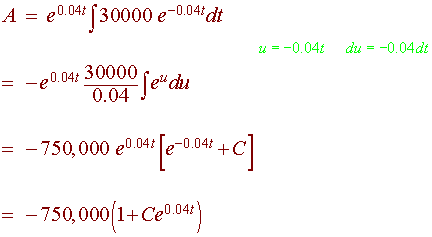
Now we use the fact that the fund currently (t  =  0) has A  =  $100,000.

        100000  =  -750000(1 + Ce^0.04(0))

        100000  =  -750000(1 + C)

        C  =  -1.1333

We can now find out how much will be in the account in t  = 10 years.

        A(10)  =  -750000(1 - 1.1333e^0.04(10))  =  741,828

The account will be worth $741,828 in ten years.

Back to the Math 117 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions