Applications of Differential Equations

Applications of Differential Equations

Anytime that we a relationship between how something changes, when it is changes, and how much there is of it, a differential equations will arise. Applications include population dynamics, business growth, physical motion of objects, spreading of rumors, carbon dating, and the spreading of a pollutant into an environment to name a few.

Population Growth

The current population of California is 36 million with a 33% Hispanic population. The rate of people entering the state, by being born or immigrating, is approximately 1 million people per year with 70% of the newcomers Hispanic. The rate of departure of the population, by dying or emigrating, is approximately 0.2 million people per year. Assume that the departing population has the same ethnic mix as California's population at the time of departure. In 20 years, what percent of California will be Hispanic?

Solution

We use a useful fact applicable to any question where there is input and output through a system:

Total Rate = Rate In - Rate Out

In this case, if we let x represent the number of Hispanics in the state and t represent the time in years from now, then we have

                                   dx
        Total Rate =
                                   dt

The rate in will be 70% of 1 million or

Rate In = 0.7(1) = 0.7

The rate out is more difficult. At time t, there are x Hispanics in California. To find the population of California, we take the initial population plus the added population per year times the number of years. Since there are 1 million people entering and 0.2 million leaving the population at time t is

P(t) = 36 + (1 - 0.2)t = 36 + 0.8t

Hence the rate of Hispanics leaving can be found by multiplying the proportion of Hispanics in the state and the rate of people leaving the state.

                                    Number of Hispanics
        Rate Out     =                                               * Rate of all leaving California
                                   Number of Californians

                                        x
        Rate Out     =                        * 0.2
                                  36 + 0.8t

We use the Rate In and Rate Out information to get

          dx                             0.2 x
                    =    0.7 -
          dt                           36 + 0.8t

We can rewrite this as

          dx                  0.2
                    +                      x    =    0.7
          dt               36 + 0.8t

This is a first order linear differential equation with

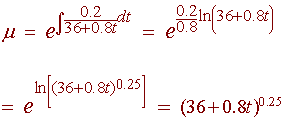
The solution is

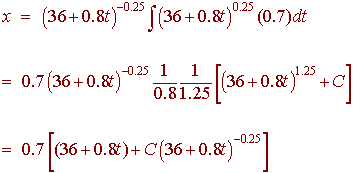
Now we have that at time zero, there are 33% of 36 million Hispanics or 11.88 million Hispanics, hence

Solving for C gives

C = -46.61

Now plug in 20 for t to get

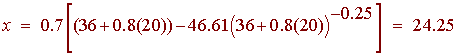
This is the number of Hispanics that will be living in California. To arrive at the percent we divide it by California's population in twenty years.

P(20) = 36 + (0.8)(20) = 52

Finally we have

            24.25
                            =   0.47
              52

Our model predicts that California will be 47% Hispanic in 20 years.

Poison Concentration

At age sixteen an addict has a concentration of a drug related poison of C. If the addict takes the drug regularly for a year, then the concentration of the drug is given by

        dC
                   = A - BC
        dt

Where A is the rate into the bloodstream and BC is the rate out. Determine a formula for the concentration in terms of A and B.

Solution

We separate variables

           dC
                        = dt
        A - BC

Now integrate both sides to get

            1
        -        ln| A - BC| = t + k₁
            B

Multiply by -B and rename the constant to get

ln|A - BC| = -t + k₂ k₂ = -Bk₁

A - BC = e^{-t + k2} = e^-t e^k2 = k₃e^-t

Now subtract A and divide by -B to get

C = ke^-t + A/B

Back to the Math 117 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions