Lagrange Multipliers

Lagrange Multipliers

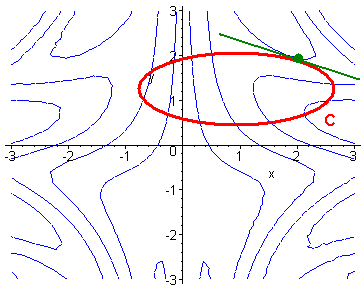
Suppose that we have a function f(x,y) that we want to maximize in the restricted domain g(x,y) = c for some constant c.  Then we can look at the level curves of f and seek the largest level curve that intersects the curve g(x,y) = c.  It is not hard to see that these curves will be tangent.  Hence the gradient vectors will be parallel.

       

Theorem Let f(x,y) be differentiable and g(x,y) = c define a smooth curve.  Then the maximum and minimum of f subject to the constraint g occur at the critical points of           F(x,y)  =  f(x,y) - l g(x,y) for some constant l.

Example:

Find the extrema of 

        f(x,y) = x² - y² 

subject to the constraint 

        y - x² = 0

Solution:  

We have 

        F(x,y)  =   (x² - y²) - l (y - x²) 

Now take partial derivatives and set them equal to zero:

        F_x(x,y)  =  2x - l2x  =  0

        F_y(x,y)  =  -2y - l  =  0

This gives us the three equations:

        2x = -l2x,    -2y = l(1),     and    y - x² = 0

the first equation gives us (for x nonzero)
 

        l = -1

Hence the second equation becomes

        -2y = -1 

so that 

        y = 1/2

the third equation gives us

        1/2 - x² = 0

Hence

        x = /2

For x = 0, we see that y = 0.  Hence the two possible local extrema are 

        (/2,1/2)    and    (0,0)

Plugging into f(x,y), we see that

        f(/2,1/2) = 1/4

and 

        f(0,0) = 0

Hence 1/4 is the local maximum and 0 is the local minimum.

Example 2

Find the distance from the origin to the surface 

        xyz = 8

Solution

We minimize 

        D = x² + y² + z²  

subject to the constraint

        xyz = 8

We have

        F(x,y)  =   ( x² + y² + z²) - l (xyz) 

Now take partial derivatives and set them equal to zero:

        F_x(x,y)  =  2x - lyz  =  0

        F_y(x,y)  =  2y - lxz  =  0

        F_z(x,y)  =  2z - lxy  =  0

Which give the four equations

        2x = l yz,        2y = lxz,        2z = lxy,    xyz  =  8

or

        l = 2x/yz = 2y/xz = 2z/xy        xyz  =  8

or 

        2x² = 2y² = 2z²        xyz  =  8

Hence 

        x = ± y = ± z

Plugging into the last equations gives 

        ±x³ = 8    or    x = ±2

We get the points 

        (2,2,2), (2,-2,-2), (-2,-2,2), (-2,2,-2)

these all have distance from the origin.

Two Constraints

Example:

Maximize 

        x² + y² + z²   

on the intersection of the two surfaces:

        xyz = 1    and     x² + y² + 2z² = 4

Solution:

When there are two constraints we use

        F(x,y,z)  =  f(x,y,z) - ag(x,y,z) + bh(x,y,z)

and find the critical points of F.  We get

        F(x,y,z)  =  (x² + y² + z²) - a(xyz) - b(x² + y² + 2z²)

and take partial derivatives

        F_x  =  2x - ayz - b2x   
        F_y  =  2y - axz - b2y   
        F_z  =  2z - axy - b4z   

which gives the five equations

        2x = ayz + 2bx,     2y = axz + 2by,     2z = axy + 4bz,    

        xyz = 1,   and     x² + z = 1

Multiply the first equation by x, the second by y and the third by z to get

        2x² = axyz + 2bx²,     2y² = axyz + 2by²,     2z² = axyz + 4bz²,

Solving each for axyz gives

        axyz = 2x²  - 2bx² = 2y²  - 2by² = 2z²  - 4bz²  

This gives that 

        2x²(1 - b) = 2y²(1 - b) = 2z² (1 - 2b)

This first equality gives

        x = ±y

Using the last of the original equations to solve for x² gives

        x²  = 1 - z

Substituting and dividing by 2 gives

        (1 - z)(1 - b) = z² (1 - 2b)

Using xyz  =  1 and substituting gives

        ±(1 - z)z  =  1

so

        z² - z + 1  =  0    or    z² + z - 1  =  0

The first has no solution and the second has solutions

        z  =  -1/2 ± 1/2

Now

       

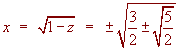
and

       

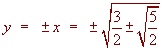
Back to the Math 117 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions