Name
MATH 116
PRACTICE MIDTERM 1
Please work out each of the given problems.
Credit will be based on the steps that you show towards the final answer.
Show your work.
PROBLEM 1 Find the derivative of the following functions
A.
f(x) = ln(ln x)
Solution
u = ln x u' = 1/x
f(u) = ln u f '(u) = 1/u
We get
1
1
1
f '(x)
=
=
x ln
x
x ln x
Solution
![]()
and use the chain and product rules. We have
u = ex ln x u' = ex ln x + ex / x
f(u) = eu f '(u) = eu
so that
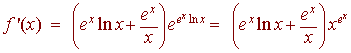
Solution
![]()
now the derivative is simply
f '(x) = 1
PROBLEM 2
Find the following anti-derivatives.
A.
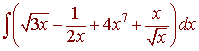
Solution
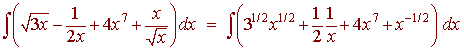
Now we use the power rule for integration to get
2/3 31/2 x3/2 + 1/2 ln|x| + 1/2 x8 + 2x1/2 + C
Solution
For this integral, we use u-substitution. We let
u = 4 - 3x5 du = -15x4 dx
We get
![]()
Solution
u = x + ex du = 1 + ex
We get
![]()
PROBLEM 3
During an experiment with a deadly new virus, Tom
drops a flask of the virus on the floor. Tom
and his four lab aids are immediately infected.
During the next six hours they infect an additional forty unsuspecting
people. Assume the rate of
spreading of the virus is proportional to the number of people who have been
infected.
A. Write a differential equation that models
this situation. Be sure to label
your variables.
Solution
We let
t = the time in hours after the flask is dropped
P(t) = the number of people infected after t hours
Then
dP
= kP P(0) =
5 P(6) = 45
dt
B. How long will it be until one million
people have been infected?
Solution
Since this is the standard exponential growth model, the solution to the differential equation is
P = P0 ekt
Since P(0) = 5, we have P0 = 5 Hence
P = 5 ekt
Now use the fact that P(6) = 45 to get
45 = 5 e6k
9 = e6k
ln 9 = 6k
ln 9
k =
= 0.3662
6
Hence
P = 5 e0.3662t
We want the time when P = 1,000,000. We write
1,000,000 = 5 e0.3662t
200,000 = e0.3662t
ln 200,000 = 0.3662 t
ln 200,000
t =
= 33.3
0.3662
We can conclude that there will be 1,000,000 people infected in less than 34 hours.
PROBLEM 4 A population of bacteria is growing at the rate of
dP
3000
=
dt
1 + 0.25t
where t is the time in
days. When t
= 0, the population is 1000.
A. Write an equation that models the population P
in terms of the time t.
Solution
We need to solve the integral
![]()
We let
u = 1 + 0.25t du = 0.25 dt
We have
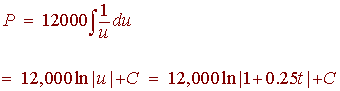
We have P(0) = 1000. Hence
1000 = 12,000 ln|1 + 0.25(0)| + C
1000 = 12,000 ln|1| + C = 12,000 (0) + C
C = 1000
We can conclude that
P(t) = 12,000 ln|1 + 0.25 t| + 1000
B. What is the population after 3
days?
Solution
We plug in 3 for t to get
P(3) = 12,000 ln|1 + (0.25)(3)| + 1000 = 7715
We can conclude that the population will be 7715 after 3 days.
C. After how many days will the population be 12,000?
Solution
We set P = 12,000 and solve for t.
12,000 = 12,000 ln|1 + 0.25 t| + 1000
11,000 = 12,000 ln|1 + 0.25 t|
11/12 = ln|1 + 0.25 t|
e11/12 = 1 + 0.25 t
e11/12 - 1 = 0.25 t
t = 4(e11/12 - 1) = 6
We can conclude that after 6 days, the population will be 12,000.
Extra Credit:
Write
down one thing that your instructor can do to make the class better.