Math 116 Practice Final
Please work out each of the given problems. Credit will be based on the steps that you show towards the final answer. Show your work
Problem 1 Find the derivative of the following functions
A. f(x) = ln(ln(1 - x))
B.
![]()
C.
ex
f(x) =
sin
x
Problem 2 Evaluate the following integrals
A.
![]()
B.
![]()
C.
![]()
D.
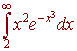
E.
![]()
Problem 3
Find the volume of the solid formed by revolving the region bounded by the curves
y = x2 + 4 and y = 5x
about the x-axis.
Problem 4
In 1980 there were 200 reported cases of the HIV virus and in 1984, there were 200,000 reported cases. Is has been predicted that the number of HIV cases will eventually level off at about 80,000,000. Determine how many cases this model predicts for the year 2003 by solving the differential equation
dP
= P(80,000,000 - P)
dt
Problem 5
The GNP growth since 1980 can be modeled by the equation
y = 3 cos(0.8t) + 2
A. Find the period of this function and explain what this says about growth.
B. What is the maximum growth and when does it occur? (Use calculus to show this).
Problem 6
The rate of which a pill is dissolved when it enters the body is given by
dy
et
=
dt
1 + t2
Use Simpson's Rule with n = 4 to determine the total amount of the pill that is dissolved during the first 4 minutes.
Problem 7
Find the area between the curves
y = ln x y = sin x x = 1 and x = 2