Integrals of Trigonometric Functions
Six Important Integrals Involving Trig Functions
In the previous discussion we gave the derivatives of the six basic trig functions. Since integrals are antiderivatives, we can read the table backwards and arrive at six basic trig integrals. We list the table again, adjusting with a "+ C".
|
|
f (x) |
| sin x + C | cos x |
| cos x + C | -sin x |
| tan x + C | sec2 x |
| sec x + C | sec x tan x |
| csc x + C | -csc x cot x |
| cot x + C | -csc2 x |
Example
Find
![]() sec(2x)tan(2x)
dx
sec(2x)tan(2x)
dx
Solution
This does not exactly fit the table, however with a u-substitution we can adjust. Let
u = 2x du = 2dx dx = 1/2 du
Substituting, gives
1/2 ![]() sec
u tan u du
sec
u tan u du
Now we can recognize this as the derivative of sec u, hence the integral is
1/2 sec u + C = 1/2 sec(2x) + C
Exercise
Evaluate the following integrals (Hold your mouse on the yellow rectangle for the answer)
A. ![]() sin
x sec2(cos x) dx
sin
x sec2(cos x) dx ![]()
B. ![]() x
csc(x2)cot(x2) dx
x
csc(x2)cot(x2) dx
![]()
The Integrals of the Six Basic Trig Functions
Now that we know what integrals produce the six basic trig functions, we would like to know how to find the integrals of the six basic trig functions. While sin x and cos x come straight from the antiderivatives, the other four are more difficult to find. We begin with tan x.
![]() tan
x dx
tan
x dx
The trick to find this integral is to use the sin over cos definition of the tan. We have
![]()
Now we can use u-substitution. Let
u = cos x du = -sin x dx
This gives us
-![]() 1/u
du = -ln|u| + C = -ln|cos x| + C
1/u
du = -ln|u| + C = -ln|cos x| + C
![]() sec
x dx
sec
x dx
This one is even trickier. We multiply by the term
sec x + tan x
sec x + tan x
I know, that is just what you were thinking of. We have
![]()
and behold! The numerator is the derivative of the denominator. This leads us to the substitution
u = sec x + tan x du = (sec x tan x + sec2 x) dx
Now substitute to get
![]() 1/u
du = ln|u| + C = ln|sec x + tan x| + C
1/u
du = ln|u| + C = ln|sec x + tan x| + C
![]() csc
x dx
csc
x dx
This integral is most easily accomplished by using the trig identity
csc x = sec(p/2 - x)
We have
![]() csc
x dx =
csc
x dx = ![]() sec(p/2
- x) dx
sec(p/2
- x) dx
Let
u = p/2 - x du = -dx
This gives us
-![]() sec(u)
du = - ln|sec u + tan u| + C
sec(u)
du = - ln|sec u + tan u| + C
Now resubstitute to get
-ln|sec(p/2 - x) + tan(p/2 - x)| + C
and use the trig identities again to get
-ln|csc x + cot x| + C
Exercise
Show that
![]() cot
x dx = ln|sin x| + C
cot
x dx = ln|sin x| + C
We summarize with the following table
|
f(x) |
|
| sin x | -cos x + C |
| cos x | sin x + C |
| tan x | -ln|cos x| + C |
| sec x | ln|sec x + tan x| + C |
| csc x | -ln|csc x + cot x| + C |
| cot x | ln|sin x| + C |
Application
An adult on a tread mill has a respiratory cycle with air flow approximately
pt
v = |1.4sin
|
2
where t is the time in seconds and v is the velocity in liters per second. Find the volume of air inhaled during one cycle.
Solution
The integral of the velocity will give the total volume inhaled. One cycle goes from 0 to 2 seconds. We have
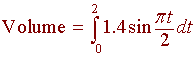
Let
u = p t/2 du = p/2 dt dt = 2/p du
when
t = 0 u = 0
and when
t = 2 u = p
We get
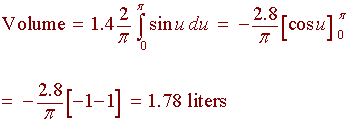
The volume of air in one cycle is about 1.78 liters.
Back to the Math 116 Home Page
Back to the Math Department Home
e-mail Questions and Suggestions