Derivatives of the Trigonometric Functions
Derivative of f(x) = sin(x)
First note that angles will always be given in
radians. Degrees and calculus never go together. If you ever hear
the word "Degree" used in this class the appropriate question to ask
is "Do you mean Celsius or Fahrenheit?"
We begin by exploring an important limit. We can graph the function
sin x
f(x) =
x
The graph is given below
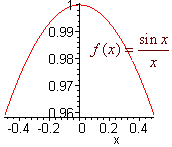
The graph clearly indicates that as x approaches 0, y approaches 1. We will use this fact in to find the derivative of f(x) = sin x. The fact can be proven using triangles, but that should be done in a more advanced course. Another important limit that help in the proof is
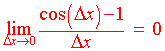
Once again, we will not prove this fact. It can be found in more advanced textbooks.
|
d |
Proof:
We use the limit definition of the derivative along with
the sum of angles formula for sin x.
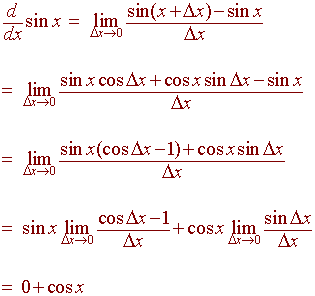
Example
Find the derivative of
f(x) = x2 sin(3x)
Solution
We use the product and the chain rules.
f '(x) = (2x)(sin(3x)) + (x2)(3cos(3x))
= 2x sin(3x) + 3x2 cos(3x)
The Other Trigonometric Functions
We can find the derivatives of the other five trigonometric functions by using trig identities and rules of differentiation. Below is a list of the six trig functions and their derivatives.
| f(x) | f '(x) |
| sin x | cos x |
| cos x | -sin x |
| tan x | sec2 x |
| sec x | sec x tan x |
| csc x | -csc x cot x |
| cot x | -csc2 x |
We will prove two of these.
The proof to the derivative of cos x
We use the identity
cos x = sin(p/2 - x)
Take the derivative of both sides using the chain rule for the derivative of the right hand side.
(cos x)' = - cos(p/2 - x)
Now use the identity
sin x = cos(p/2 - x)
to arrive at the result
(cos x)' = - sin x
The proof to the derivative of tan x
We use the quotient rule on
sin x
tan x =
cos x
(cos x)(cos x) - (sin x)(-sin x)
(tan x)'
=
cos2 x
cos2 x + sin2
x
1
=
=
= sec2 x
cos2
x
cos2 x
Application
The amount A of food available at day t of the year for a North American hare can be modeled by the equation
2p(t - 120)
A(t) = 320 cos
365
On what day does the hare have the most food available?
Solution
We are asked to find a maximum, which involves taking the first derivative and setting it equal to zero. We have
-320(2p)
2p(t - 120)
A'(t) =
sin
365
365
Setting it equal to zero and solving gives us
2p(t - 120)
= kp
365
When k = 0, we get t = 120 and when k = 1 we get t = 302.5. The second derivative test will tell us that t = 120 gives us a maximum and t = 320 gives us a minimum. Other values of k will give us the same day of the year. We can conclude that the hare has the greatest food supply on April 30.
Back to the Math 116 Home Page
Back to the Math Department Home
e-mail Questions and Suggestions