Substitution 

Substitution (Definition)

Recall that the chain rule states that

        [f(g(x))]'   =   f '[g(x)] g'(x)

For example, 

        (1 - x²)⁷ '  =  7(1 - x²)⁶ (-2x)

The goal of this discussion is to learn how to go backwards.  This process is called integration by substitution.  In general we have

Examples

Example

Calculate

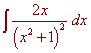
Solution

Let 

        u =  x² +1

        du/dx  =  2x     or     du  =  2x dx

We substitute:

        u ^-2 du  =  -u ^-1 + C  =  -(x² + 1) ^-1 + C

Steps in Substitution

1. Find the function derivative pair (f and f ').
   
   

2. Let u = f(x).
   
   

3. Find du/dx and adjust for constants.
   
   

4. Substitute.
   
   

5. Integrate.
   
   

6. Resubstitute.

Example

Integrate

        x (x² + 4)¹⁰⁰ dx

Solution

The difficulty with this is that the derivative of x² + 4 is 2x not x.  We can overcome this by multiplying and dividing by 2

        x (x² + 4)¹⁰⁰ dx  = 1/2 2x (x² + 4)¹⁰⁰ dx

Now we can use substitution.  Let  

        u  =  x² + 4        du  =  2x dx

The integral becomes

        1                         1     1
            u¹⁰⁰ du  =                u¹⁰¹ + C
        2                         2   101

                1
        =           (x² + 4)¹⁰¹ + C
              202

Example

Integrate

        (x² + 2)² dx

Solution

The difficulty with this is that the derivative of x² + 2 is 2x.  There is more than a constant that we are lacking.  The method of substitution will not work here.  Instead, we use some algebra (FOIL).

        (x² + 2)² dx  =   (x⁴ + 4x² + 4) dx

Now we can use the power rule to get

        =  1/5 x⁵ + 4/3 x³ + 4x + C

Exercises

Integrate

A. x² (x³ + 6) ^-5 dx          

B.         

Back to the Math 116 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions