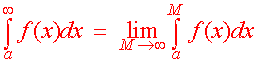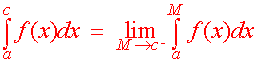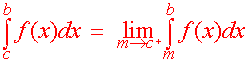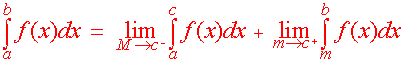Improper Integrals
Integrals with Infinite Limits
Up until now, all the integrals that we have performed have had finite limits
and integrands with no asymptotes. Now we will investigate integrals with
infinite limits and integrands with vertical asymptotes. We begin with
infinite limits.
|
Integrals with Infinity as a Limit
|
Note: A similar definition applies to integral with negative infinity as a limit.
Example
Evaluate
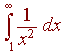
Solution
We use the definition to find
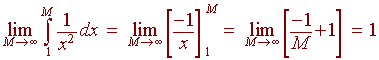
Integrals with Vertical Asymptotes
The fundamental theorem of calculus tells us how to evaluate integrals if the
functions is continuous. Id does not apply if the function has a vertical
asymptote. In this case we will need to make an adjustment. The
definition below tells us how the make this adjustment.
Definition
A.
B.
C.
|
Example
Evaluate
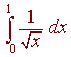
Solution
The
integrand has a vertical asymptote at x = 0, so we must use part B
if the definition. We have
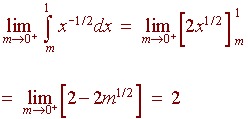
Application
Statisticians are always taking about the normal or bell curve. This curve is defined by the function
![]()
Where m is the mean of the distribution and s is the standard deviation. With a probability distribution of f(x), the probability of an event occurring between a and b is given by
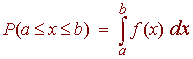
Example
The weight of a species of rodent is normally distributed with mean 0.5 kg and standard deviation 0.1 kg. What is the probability of a randomly selected specimen to have a weight of greater then 0.6 kg?
Solution
Since we are not given an upper bound on the weight, we use infinity for the upper limit. We have
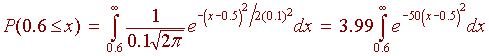
This is an improper integral such that there is no simple antiderivative. We use an approximation technique to solve it such as the Midpoint Rule or Simpson's Rule or a calculator to get an answer of 0.1586.
Author's Note: I put this into the TI 89 calculator which produced the above number with a warning of "questionable accuracy".
Back to the Math 116 Home Page
Back to the Math Department Home
e-mail Questions and Suggestions