Advanced Substitution

 

Substituting x

 

Example

Find

       

 

Solution

Notice first that the square root is what makes this problem difficult.  Hence we let

        u  =  x - 1         du  =  dx

This seems not to get rid of the x term, but notice that if we add 1 to both sides, we get

        x  =  u + 1

Now we can substitute to get

         

        =  2/5 u5/2 + 2/3 u3/2 + C  

        =  2/5 (x - 1)5/2 + 2/3 (x - 1)3/2 + C

 

Exercises:  

Find the following integrals

       

        -x - ln | 1 - x | + C        -ln | 1 - x | + 2(1 - x) - 1/2 (1 - x)^2 + C        1/2 [ (1 - x^2) - ln | l - x^2 | ]+ C

 

Summary of Substitution

A list of "good u's" follows:

A.  Inside the parentheses

B.  In the square root

C.  The denominator

E.  In the exponential

F.  Be creative

 

 

Definite Integrals

We can use substitution to evaluate definite integrals.  When using substitution, we substitute the values for u and do not resubstitute at the end.

 

Example

Evaluate

       

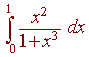
Solution

This is a substitution with 

        u  =  1 + x3         du  =  3x2 dx        1/3 du  =  x2 dx

This is just old substitution business.  The new part is how to deal with the limits 0 and 1.  We just plug into x and find u.

        When      x  =  0        u  =  1 + 03  =  1

        When      x  =  1        u  =  1 + 13  =  2

Now we can substitute all the numbers and expressions to get

       

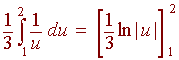
Now we just plug in the numbers 2 and 1.  Notice that there is no " + C" since it is a definite integral.  We also do not need to resubstitute since the numbers already represent "u" values.  Plugging in gives

        1/3 ( ln 2  -  ln 1)  =  1/3 ln 2

 

Back to the Math 116 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions